Plantilla:Máximo común divisor
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 07:52 20 feb 2009 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 19:24 7 oct 2014 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 11: | Línea 11: | ||
| <center><math>m.c.d.(24,60)= 2^2 \cdot 3=12</math></center> | <center><math>m.c.d.(24,60)= 2^2 \cdot 3=12</math></center> | ||
| }}{{p}} | }}{{p}} | ||
| - | {{AI2|titulo=Actividad Interactiva: ''m.c.d.''|cuerpo= | ||
| - | {{ai_cuerpo | ||
| - | |enunciado=1. Calcula el m.c.d. de dos números. | ||
| - | |actividad= | ||
| - | Calcula mentalmente y anota en tu cuaderno el máximo común divisor de estos dos números; márcalo en la ventana del control inferior y pulsa intro. | ||
| - | Si necesitas ayuda pulsa sobre los triángulos del control de arriba y verás la descomposición factorial de cada número, pero en ese caso el mensaje ENHORABUENA tendrá otro color. | ||
| - | |||
| - | Cada vez que pulses sobre "inicio" aparecerán otros dos números aleatoriamente. | ||
| - | |||
| - | <center><iframe> | ||
| - | url=http://maralboran.org/web_ma/descartes/1y2_eso/Multiplos_divisores/mcd2n_1.html | ||
| - | width=410 | ||
| - | height=410 | ||
| - | name=myframe | ||
| - | </iframe></center> | ||
| - | <center>[http://maralboran.org/web_ma/descartes/1y2_eso/Multiplos_divisores/mcd2n_1.html '''Click''' aquí si no se ve bien la escena]</center> | ||
| - | }} | ||
| - | }} | ||
| - | {{p}} | ||
| ===Propiedad=== | ===Propiedad=== | ||
Revisión de 19:24 7 oct 2014
El máximo común divisor (m.c.d.) de dos o más números es el mayor de todos los divisores comunes a esos números.
Para obtenerlo se descomponen los números en factores primos y se toman los factores comunes elevados al menor exponente.
Ejemplo: m.c.d.
- Calcula el m.c.d.(24,60).
Solución:
Descomponemos 24 y 60 en sus factores primos:
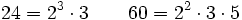
Multiplicando los factores comunes elevados al menor exponente:
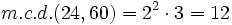
Propiedad
Si a es múltiplo de b, entonces m.c.d.(a,b)=b.
Por ejemplo, m.c.d.(15, 30)=15.
Números primos entre sí
Dos números son primos entre sí, si su m.c.d. es 1.
Por ejemplo, 6 y 11 son primos entre sí.

