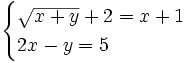Ejercicios: Álgebra (1ºBach)
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 11:15 14 oct 2014 Coordinador (Discusión | contribuciones) (→Control de ejemplo) ← Ir a diferencia anterior |
Revisión de 11:20 14 oct 2014 Coordinador (Discusión | contribuciones) (→Control de ejemplo) Ir a siguiente diferencia → |
||
| Línea 22: | Línea 22: | ||
| {{p}} | {{p}} | ||
| {{wolfram | {{wolfram | ||
| - | |titulo=Actividad: ''Control de Octubre 2014'' | + | |titulo=Actividad: ''Control de Octubre de 2014'' |
| |cuerpo= | |cuerpo= | ||
| {{ejercicio_cuerpo | {{ejercicio_cuerpo | ||
| Línea 31: | Línea 31: | ||
| :3) Resuelve: <math>\begin{cases} \sqrt{x+y}+2=x+1 \\ 2x-y=5 \end{cases}</math> | :3) Resuelve: <math>\begin{cases} \sqrt{x+y}+2=x+1 \\ 2x-y=5 \end{cases}</math> | ||
| :4) Resuelve: <math>9^x-3^x-6=0\,</math> | :4) Resuelve: <math>9^x-3^x-6=0\,</math> | ||
| + | :5) Resuelve: <math>\begin{cases} x^2-7x+6 \le 0 \\ -x+2>1 \end{cases}</math> | ||
| + | :6) Resuelve: <math>\frac{2^x}{3^{x+1}}=1\,</math> | ||
| {{p}} | {{p}} | ||
| |sol= | |sol= | ||
| Línea 39: | Línea 41: | ||
| :2) {{consulta|texto=solve log(x-1)+log(x+6)=log(3x+2) over the reals}} | :2) {{consulta|texto=solve log(x-1)+log(x+6)=log(3x+2) over the reals}} | ||
| :3) {{consulta|texto=solve root(x+y)+2=x+1,2x-y=5}} | :3) {{consulta|texto=solve root(x+y)+2=x+1,2x-y=5}} | ||
| - | :3) {{consulta|texto=solve 9^x-3^x-6=0 over the reals}} | + | :4) {{consulta|texto=solve 9^x-3^x-6=0 over the reals}} |
| + | :5) {{consulta|texto=solve x^2-7x+6<=0,-x+2>1}} | ||
| + | :6) {{consulta|texto=solve (2^x)/}(3^(x+1))=1 over the reals}} | ||
| {{widget generico}} | {{widget generico}} | ||
Revisión de 11:20 14 oct 2014
Menú:
| Enlaces internos | Para repasar o ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadoras |
Ejercicios resueltos
Ejercicos propuestos
- Polinomios (con solución)
- Fracciones algebraicas (con solución)
- Ecuaciones racacionales, irracionales y bicuadradas (con solución)
- Ecuaciones exponenciales (con solución)
- Inecuaciones y sistemas (con solución)
Control de ejemplo
|
Actividad: Control de Octubre de 2014
Solución: Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones:
|