Plantilla:Irracionales. Representacion
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 09:19 9 ago 2016 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 08:37 10 ago 2016 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 1: | Línea 1: | ||
| + | {{p}} | ||
| + | En la siguiente actividad vamos a ver la representación en la recta real de algunos números irracionales: | ||
| + | {{p}} | ||
| + | {{AI2|titulo=Actividades Interactivas: ''Representación de números irracionales''|cuerpo= | ||
| + | {{ai_cuerpo | ||
| + | |enunciado=1. Representación del número <math>\sqrt{2}</math>. | ||
| + | |actividad= | ||
| + | Observa en la escena la representación de <math>\sqrt{2}</math>. | ||
| + | |||
| + | #Para ello debes ir presionando sucesivamente el control pasos. | ||
| + | #Toma nota en tu cuaderno de los pasos de la representación e intenta realizarla con regla y compás. | ||
| + | #Si presionas sobre el control decimales podrás variar el número de cifras decimales. | ||
| + | {{p}} | ||
| + | <center><iframe> | ||
| + | url=http://maralboran.org/web_ma/descartes/Algebra/Irracionales/Irracionales_1.html | ||
| + | width=570 | ||
| + | height=390 | ||
| + | name=myframe | ||
| + | </iframe></center> | ||
| + | <center>[http://maralboran.org/web_ma/descartes/Algebra/Irracionales/Irracionales_1.html '''Click''' aquí si no se ve bien la escena]</center> | ||
| + | }} | ||
| + | {{ai_cuerpo | ||
| + | |enunciado=2. Representación del número de oro <math>\phi=\cfrac{1+\sqrt{5}}{2}</math>. | ||
| + | |actividad= | ||
| + | Desde la antigüedad matemáticos filósofos y artistas han creído en la existencia de una razón privilegiada, que fue llamada número áureo. | ||
| + | |||
| + | Los griegos consideraban que un rectángulo cuyos lados <math>a\;\!</math> y <math>b\;\!</math> están en la razón <math>\cfrac{a}{b} = \phi</math> es especialmente armonioso. Esta proporción de medidas se ha utilizado con mucha frecuencia en el arte. | ||
| + | |||
| + | Es el primer número irracional del que se tuvo conciencia de que lo era. | ||
| + | |||
| + | En la escena puedes ver la representación del número de oro <math>\phi=\cfrac{1+\sqrt{5}}{2}</math> basada en una construcción gráfica que se encuentra en un libro de Euclídes (siglo III a. J.C.). | ||
| + | |||
| + | #Para ello debes ir presionando sucesivamente el control pasos. | ||
| + | #Toma nota en tu cuaderno de los pasos de la representación e intenta realizarla con regla y compás. | ||
| + | #Si presionas sobre el control decimales podrás variar el número de cifras decimales. | ||
| + | {{p}} | ||
| + | <center><iframe> | ||
| + | url=http://maralboran.org/web_ma/descartes/Algebra/Irracionales/Irracionales_2.html | ||
| + | width=570 | ||
| + | height=390 | ||
| + | name=myframe | ||
| + | </iframe></center> | ||
| + | <center>[http://maralboran.org/web_ma/descartes/Algebra/Irracionales/Irracionales_2.html '''Click''' aquí si no se ve bien la escena]</center> | ||
| + | }} | ||
| + | {{ai_cuerpo | ||
| + | |enunciado=3. Representación de otras raíces cuadradas. | ||
| + | |actividad= | ||
| + | Observa en la escena la representación de otras raices cuadradas. | ||
| + | |||
| + | #Pulsando sobre el control pasos puedes observar cómo se representa la raíz cuadrada de cualquier número entero. | ||
| + | #Representa en tu cuaderno la raíz de 3 y la raíz de 5. | ||
| + | #Pulsando el control decimales puedes obtener el número de ellos que desees. | ||
| + | #Utiliza el botón Limpiar si quieres ver con más claridad la representación de algún número. | ||
| + | |||
| + | <center><iframe> | ||
| + | url=http://maralboran.org/web_ma/descartes/Algebra/Irracionales/Irracionales_3.html | ||
| + | width=570 | ||
| + | height=390 | ||
| + | name=myframe | ||
| + | </iframe></center> | ||
| + | <center>[http://maralboran.org/web_ma/descartes/Algebra/Irracionales/Irracionales_3.html '''Click''' aquí si no se ve bien la escena]</center> | ||
| + | }} | ||
| + | }} | ||
| + | {{p}} | ||
| {{Geogebra_enlace | {{Geogebra_enlace | ||
| |descripcion=En esta escena podrás ver como se representan gráficamente los números del tipo <math>\sqrt{n},~n \in \mathbb{N}</math>. | |descripcion=En esta escena podrás ver como se representan gráficamente los números del tipo <math>\sqrt{n},~n \in \mathbb{N}</math>. | ||
| |enlace=[http://ggbm.at/tEx3VB9x Representación de números irracionales] | |enlace=[http://ggbm.at/tEx3VB9x Representación de números irracionales] | ||
| }} | }} | ||
Revisión de 08:37 10 ago 2016
En la siguiente actividad vamos a ver la representación en la recta real de algunos números irracionales:
|
Actividades Interactivas: Representación de números irracionales
1. Representación del número
 . .Actividad: Observa en la escena la representación de  . .
2. Representación del número de oro
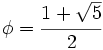 . .Actividad: Desde la antigüedad matemáticos filósofos y artistas han creído en la existencia de una razón privilegiada, que fue llamada número áureo. Los griegos consideraban que un rectángulo cuyos lados Es el primer número irracional del que se tuvo conciencia de que lo era. En la escena puedes ver la representación del número de oro
3. Representación de otras raíces cuadradas.
Actividad: Observa en la escena la representación de otras raices cuadradas.
|
En esta escena podrás ver como se representan gráficamente los números del tipo 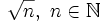 .
.
 y
y  están en la razón
están en la razón 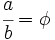 es especialmente armonioso. Esta proporción de medidas se ha utilizado con mucha frecuencia en el arte.
es especialmente armonioso. Esta proporción de medidas se ha utilizado con mucha frecuencia en el arte.

