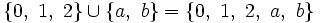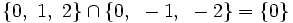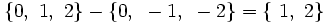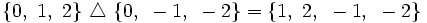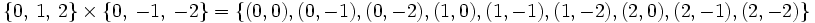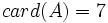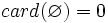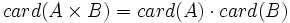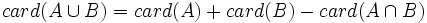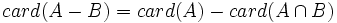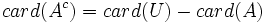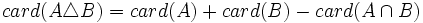Conjuntos
De Wikipedia
| Revisión de 11:45 11 ago 2016 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 11:48 11 ago 2016 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 45: | Línea 45: | ||
| Un conjunto está definido únicamente por los elementos que lo componen, y no por la manera en la que se lo representa. Por ello, la relación de igualdad entre conjuntos se define como: | Un conjunto está definido únicamente por los elementos que lo componen, y no por la manera en la que se lo representa. Por ello, la relación de igualdad entre conjuntos se define como: | ||
| {{Caja_Amarilla|texto=Dos conjuntos A y B, son iguales (A=B) si y sólo si tienen los mismos elementos '''(Axioma de extensionalidad)'''.}} | {{Caja_Amarilla|texto=Dos conjuntos A y B, son iguales (A=B) si y sólo si tienen los mismos elementos '''(Axioma de extensionalidad)'''.}} | ||
| - | |celda2=<center>[[Imagen:elementos_cto.png|thumb|250px|Fig.2 - Relación de pertenencia]]</center> | + | |celda2=<center>[[Imagen:elementos_cto.png|thumb|250px|Fig.2 - '''Relación de pertenencia''']]</center> |
| }} | }} | ||
| {{p}} | {{p}} | ||
| + | {{Tabla75|celda1= | ||
| {{Teorema_sin_demo|titulo=Consecuencias del axioma de extensionalidad | {{Teorema_sin_demo|titulo=Consecuencias del axioma de extensionalidad | ||
| |enunciado= | |enunciado= | ||
| Línea 61: | Línea 62: | ||
| {{p}} | {{p}} | ||
| === Relación de inclusión. Subconjuntos === | === Relación de inclusión. Subconjuntos === | ||
| - | {{Tabla75|celda1= | ||
| {{Caja_Amarilla|texto= | {{Caja_Amarilla|texto= | ||
| *Un conjunto B es un '''subconjunto''' del conjunto A si cada elemento de B es a su vez un elemento de A. Lo denotaremos <math> B \subseteq A</math>. También puede escribirse <math> A \supseteq B</math> y decirse que B está incluido en A, que A contiene a B, que B está contenido en A, que A incluye a B o que A es un '''superconjunto''' de B. | *Un conjunto B es un '''subconjunto''' del conjunto A si cada elemento de B es a su vez un elemento de A. Lo denotaremos <math> B \subseteq A</math>. También puede escribirse <math> A \supseteq B</math> y decirse que B está incluido en A, que A contiene a B, que B está contenido en A, que A incluye a B o que A es un '''superconjunto''' de B. | ||
| Línea 74: | Línea 74: | ||
| *<math> \{1,~ 3 \} \subset \{ 1,~ 2,~ 3,~ 4 \}</math> | *<math> \{1,~ 3 \} \subset \{ 1,~ 2,~ 3,~ 4 \}</math> | ||
| }} | }} | ||
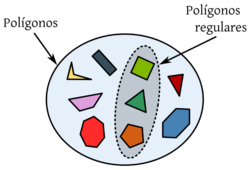
| - | |celda2=[[Imagen:cto.png|thumb|250px|Fig.3 - Representación de la relación de inclusión mediante diagrama de Venn. Los diversos polígonos en la imagen constituyen un conjunto. Algunos de los elementos del conjunto, además de ser polígonos son regulares. La colección de estos últimos es otro conjunto, en particular, un subconjunto del primero.]] | + | |celda2=[[Imagen:cto.png|thumb|250px|Fig.3 - '''Representación de la relación de inclusión mediante diagrama de Venn:''' Los diversos polígonos en la imagen constituyen un conjunto. Algunos de los elementos del conjunto, además de ser polígonos son regulares. La colección de estos últimos es otro conjunto, en particular, un '''subconjunto''' del primero.]] |
| }} | }} | ||
| {{p}} | {{p}} | ||
Revisión de 11:48 11 ago 2016
Tabla de contenidos |
Los conjuntos son un concepto primitivo, en el sentido de que no es posible definirlos en términos de nociones más elementales, por lo que su estudio puede realizarse de manera informal, apelando a la intuición y a la lógica. Por otro lado, son el concepto fundamental de la matemática: mediante ellos puede formularse el resto de objetos matemáticos, como los números y las funciones, entre otros. Su estudio detallado requiere, pues, la introducción de axiomas y conduce a la teoría de conjuntos.
Conjuntos
Definición y notación
Conjunto vacío
El conjunto que no contiene ningún elemento se llama el conjunto vacío y se denota por 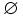 o simplemente { }.
o simplemente { }.
Conjunto universal
El conjunto universal, que denotaremos por U, es el conjunto que contiene todos los elementos posibles, dentro del contexto considerado.
Relaciones entre conjuntos
Relación de pertenecia
Un elemento se dice que «pertenece» al conjunto y se denota mediante el símbolo Relación de igualdadUn conjunto está definido únicamente por los elementos que lo componen, y no por la manera en la que se lo representa. Por ello, la relación de igualdad entre conjuntos se define como: Dos conjuntos A y B, son iguales (A=B) si y sólo si tienen los mismos elementos (Axioma de extensionalidad). |
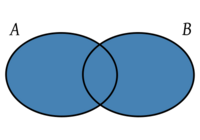
Operaciones con conjuntos
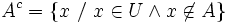
 |
Conjuntos disjuntos
Dos conjuntos A y B son disjuntos si no tienen ningún elemento en común. Es decir, su intersección es el conjunto vacio.
Cardinalidad
- Los conjuntos pueden ser finitos o infinitos. En el caso de un conjunto finito se pueden contar los elementos del conjunto. El número de elementos de un conjunto finito es su cardinal. El cardinal se denota por
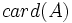 ,
, 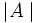 ó
ó 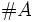 .
.
- En un conjunto infinito no hay un número finito de elementos. Es el caso, por ejemplo, de los números naturales. Sin embargo, existe una manera de comparar conjuntos infinitos entre sí, de manera que existen conjuntos infinitos «más grandes» que otros. El «número de elementos» de un conjunto infinito es un número transfinito.
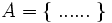 , siendo irrelevante el orden. Se puede hacer de dos maneras:
, siendo irrelevante el orden. Se puede hacer de dos maneras:
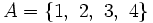
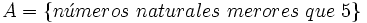 ó
ó 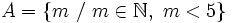

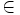 , si forma parte de él. Este símbolo lo introdujo
, si forma parte de él. Este símbolo lo introdujo 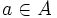 se lee «a pertenece a A». Para la noción contraria se usa el símbolo
se lee «a pertenece a A». Para la noción contraria se usa el símbolo 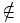 .
.

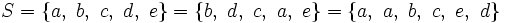
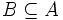 . También puede escribirse
. También puede escribirse 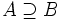 y decirse que B está incluido en A, que A contiene a B, que B está contenido en A, que A incluye a B o que A es un superconjunto de B.
y decirse que B está incluido en A, que A contiene a B, que B está contenido en A, que A incluye a B o que A es un superconjunto de B.
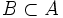 ó
ó 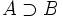
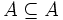
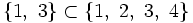
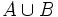 , es el conjunto de todos los elementos que pertenecen al menos a uno de los dos conjuntos.
, es el conjunto de todos los elementos que pertenecen al menos a uno de los dos conjuntos.
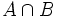 , es el conjunto de todos los elementos comunes a los dos conjuntos.
, es el conjunto de todos los elementos comunes a los dos conjuntos.
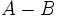 que resulta de eliminar de A cualquier elemento que esté en B.
que resulta de eliminar de A cualquier elemento que esté en B.
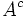 que contiene todos los elementos que no pertenecen a A, respecto a un conjunto universal U que lo contiene.
que contiene todos los elementos que no pertenecen a A, respecto a un conjunto universal U que lo contiene.
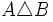 con todos los elementos que pertenecen, o bien a A, o bien a B, pero no a ambos a la vez.
con todos los elementos que pertenecen, o bien a A, o bien a B, pero no a ambos a la vez.
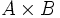 de todos los pares ordenados (a,b) formados con un primer elemento "a" perteneciente a A, y un segundo elemento "b" perteneciente a B.
de todos los pares ordenados (a,b) formados con un primer elemento "a" perteneciente a A, y un segundo elemento "b" perteneciente a B.