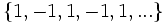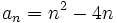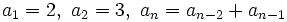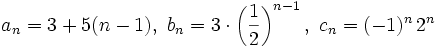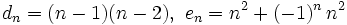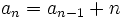Concepto de sucesión (1ºBach)
De Wikipedia
| Revisión de 10:00 14 ago 2016 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 15:31 14 ago 2016 Coordinador (Discusión | contribuciones) (→Ejercicios) Ir a siguiente diferencia → |
||
| Línea 109: | Línea 109: | ||
| {{ejercicio | {{ejercicio | ||
| - | |titulo=Ejercicios propuestos: ''Término general d una sucesión'' | + | |titulo=Ejercicios propuestos: ''Término general de una sucesión'' |
| |cuerpo= | |cuerpo= | ||
| {{ejercicio_cuerpo | {{ejercicio_cuerpo | ||
Revisión de 15:31 14 ago 2016
| Enlaces internos | Para repasar o ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadoras |
Tabla de contenidos |
Sucesión de números reales
(pág. 52)
Una sucesión de números reales es una función  , que a cada número natural
, que a cada número natural  le asocia un número real
le asocia un número real 
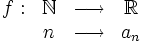
Esto genera el conjunto ordenado
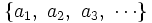
que se llaman los términos de la sucesión.
Se suele identificar a la sucesión con sus términos. Normalmente hablaremos de la sucesión de términos 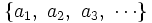 en lugar de la sucesión
en lugar de la sucesión  .
.
Ejercicios resueltos: Concepto de sucesión
- Descubre el criterio por el que se forman las sucesiones siguientes y añade dos términos más a cada una:
- a)
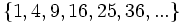
- b)
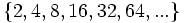
- c)
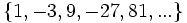
- d)
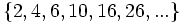
- e)
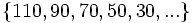
- f)
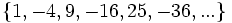
- a)
- a) Cada término es el cuadrado del lugar que ocupa.
- b) Cada término, a partir del segundo, se obtiene multiplicando por 2 el anterior.
- c) Cada término, a partir del segundo, se obtiene multiplicando por -3 el anterior.
- d) Cada término, a partir del tercero, se obtiene sumando los dos anteriores.
- e) Cada término, a partir del segundo, se obtiene restándo 20 al anterior.
- f) Los términos pares, a partir del segundo, se obtienen sumando 2 al anterior.
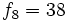
- y los términos impares, a partir del tercero, se obtienen multiplicando por 2 el anterior.
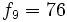
Ejercicios
(pág. 52)
|
Ejercicios propuestos: Concepto de sucesión |
Término general de una sucesión
(pág. 53)
Se llama término general de una sucesión, y se simboliza por  , al término que representa a uno cualquiera de ella. La sucesión correspondiente se representa de forma abreviada por
, al término que representa a uno cualquiera de ella. La sucesión correspondiente se representa de forma abreviada por 
- Hay veces que el término general se puede expresar mediante una fórmula:
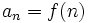 . Dándole a n un valor, se obtiene el término correspondiente.
. Dándole a n un valor, se obtiene el término correspondiente.
- Otras veces, cada término de la sucesión se obtiene a partir de operaciones con otros términos anteriores. A estas sucesiones se les llama recurrentes. En ellas, para hallar un término, tenemos que hallar todos los anteriores. En estos casos se suele dar una ley de recurrencia, una regla que relaciona cada término con sus anteriores.
Ejercicios resueltos: Término general de una sucesión
- Halla el término general (si se puede) o la ley de recurrencia de las siguientes sucesiones:
- a)
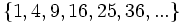
- b)
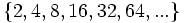
- c)
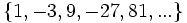
- d)
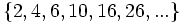
- e)
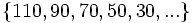
- f)
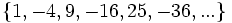
- a)
- a)
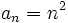
- b)
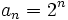
- c)
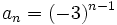
- d) Es recurrente. La ley de recurrencia es
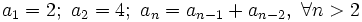
- e)
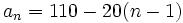
- f)
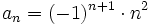
|
Actividad: Termino general de una sucesión
Solución: Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones:
|
Ejercicios
(pág. 53)
Videotutoriales
El concepto de función o aplicación ente dos conjuntos es necesario para la definición de sucesión.
- Definición de sucesión de números reales como aplicación entre el conjunto de los números naturales y el de los números reales.
- Término general de una sucesión.
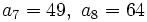
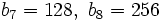
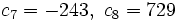
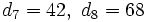
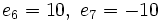
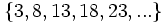
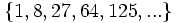
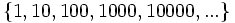
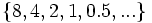
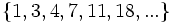
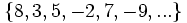
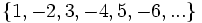
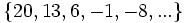
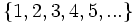 b)
b) 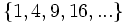 c)
c) 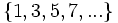
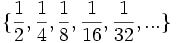 e)
e) 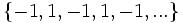 f)
f)