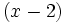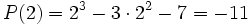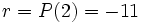Plantilla:Teorema del resto
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 17:01 16 feb 2009 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 17:09 15 ago 2016 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 26: | Línea 26: | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| - | {{AI2|titulo=Actividades Interactivas: ''Teorema del resto''|cuerpo= | ||
| - | {{ai_cuerpo | ||
| - | |enunciado='''Actividad 1:''' Selecciona la respuesta correcta. | ||
| - | |actividad= | ||
| - | |||
| - | <center><iframe> | ||
| - | url=http://contenidos.santillanaenred.com/jukebox/servlet/GetPlayer?p3v=true&xref=200411261106_AC_0_-803077230&mode=1&rtc=1001&locale=es_ES&cache=false',750,540,'snrPop',0); | ||
| - | width=100% | ||
| - | height=620 | ||
| - | name=myframe | ||
| - | </iframe></center> | ||
| - | <center>[http://contenidos.santillanaenred.com/jukebox/servlet/GetPlayer?p3v=true&xref=200411261106_AC_0_-803077230&mode=1&rtc=1001&locale=es_ES&cache=false',750,540,'snrPop',0); '''Click''' aquí si no se ve bien la escena]</center> | ||
| - | }} | ||
| - | {{ai_cuerpo | ||
| - | |enunciado='''Actividad 1:''' Halla el valor del polinomio usando el teorema del resto. | ||
| - | |actividad= | ||
| - | |||
| - | <center><iframe> | ||
| - | url=http://contenidos.santillanaenred.com/jukebox/servlet/GetPlayer?p3v=true&xref=200411261109_AC_0_-485282232&mode=1&rtc=1001&locale=es_ES&cache=false',750,540,'snrPop',0); | ||
| - | width=100% | ||
| - | height=620 | ||
| - | name=myframe | ||
| - | </iframe></center> | ||
| - | <center>[http://contenidos.santillanaenred.com/jukebox/servlet/GetPlayer?p3v=true&xref=200411261109_AC_0_-485282232&mode=1&rtc=1001&locale=es_ES&cache=false',750,540,'snrPop',0); '''Click''' aquí si no se ve bien la escena]</center> | ||
| - | }} | ||
| - | }} | ||
Revisión de 17:09 15 ago 2016
Teoerma del Resto
El valor que toma un polinomio, 
, cuando hacemos 
, coincide con el resto de la división de entre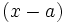 
. Es decir, 
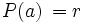, donde 
es el resto de dicha división.
Demostración:
Esto se deduce directamente de una de las propiedades de la división, la que dice que:
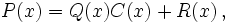
donde 
es el dividendo, 
el divisor, 
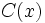el cociente y 
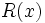el resto y verificándose además, que el grado de 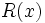es menor que el grado de .
En efecto, si tomamos el divisor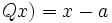 
, entonces 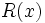tiene grado menor que 1 (el grado del resto es 0); es decir, es una constante que podemos llamar 
, y la fórmula anterior se convierte en:
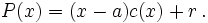
Tomando el valor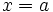 
se obtiene que:
Ejemplo: Teorema del Resto
Calcula el resto de dividir el polinomio 
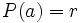
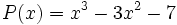entre 
Solución:
Bastará calcular 
