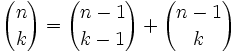Fórmula del binomio de Newton (1ºBach)
De Wikipedia
| Revisión de 09:29 4 sep 2016 Coordinador (Discusión | contribuciones) (→Triángulo de Pascal) ← Ir a diferencia anterior |
Revisión de 09:40 4 sep 2016 Coordinador (Discusión | contribuciones) (→Triángulo de Pascal) Ir a siguiente diferencia → |
||
| Línea 50: | Línea 50: | ||
| Es llamado así en honor al matemático francés [[Pascal|Blaise Pascal]], quien introdujo esta notación en 1654, en su ''Traité du triangle arithmétique''. Si bien las propiedades y aplicaciones del triángulo fueron conocidas con anterioridad al tratado de Pascal por matemáticos indios, chinos o persas, fue Pascal quien desarrolló muchas de sus aplicaciones y el primero en organizar la información de manera conjunta. | Es llamado así en honor al matemático francés [[Pascal|Blaise Pascal]], quien introdujo esta notación en 1654, en su ''Traité du triangle arithmétique''. Si bien las propiedades y aplicaciones del triángulo fueron conocidas con anterioridad al tratado de Pascal por matemáticos indios, chinos o persas, fue Pascal quien desarrolló muchas de sus aplicaciones y el primero en organizar la información de manera conjunta. | ||
| + | {{Teorema|titulo=propiedades|enunciado= | ||
| + | # El Triángulo de Pascal es simétrico. | ||
| + | # La suma de todos los valores de la fila "''n''" es igual a 2<sup>n. | ||
| + | |demo= | ||
| + | #Esto es así porque <math>{n\choose {n-p}} = {n\choose p}.</math>. | ||
| + | #Esto es debido a que, por el teorema del binomio, la expansión de la ''n''-potencia de (1 + 1)<sup>''n''</sup> = 2<sup>''n''</sup> es | ||
| + | {{p}} | ||
| + | <center><math> {n \choose 0} + {n \choose 1} + \cdots +{n \choose n-1} + {n \choose n} = 2^n, </math></center> | ||
| + | |||
| + | }} | ||
| [[Categoría: Matemáticas]][[Categoría: Números|Reales]] | [[Categoría: Matemáticas]][[Categoría: Números|Reales]] | ||
Revisión de 09:40 4 sep 2016
Binomio de Newton
Teorema: Fórmula del binomio de Newton
- El desarrollo de la potencia n-ésima de un binomio viene dado por la siguiente fórmula:
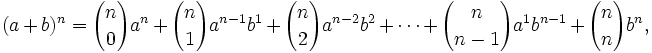
- que podemos expresar de forma abreviada de la siguiente manera:
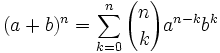
Atribuido a Newton, el teorema fue en realidad descubierto por primera vez por Al-Karaji alrededor del año 1000.
Coeficientes binomiales
Llamaremos coeficientes binomiales a los coeficientes | 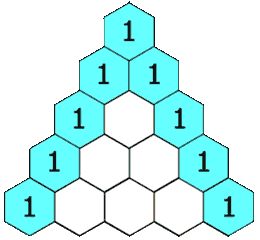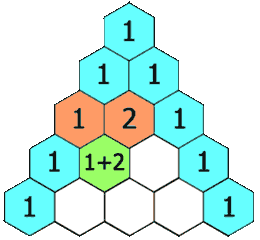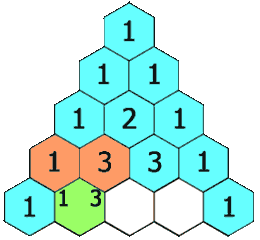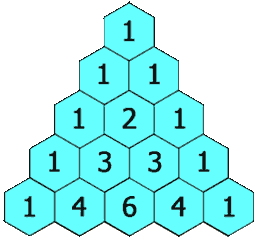
|
Triángulo de Pascal
El triángulo de Pascal es una representación de los coeficientes binomiales 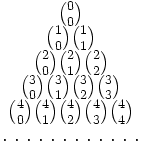
|
Es llamado así en honor al matemático francés Blaise Pascal, quien introdujo esta notación en 1654, en su Traité du triangle arithmétique. Si bien las propiedades y aplicaciones del triángulo fueron conocidas con anterioridad al tratado de Pascal por matemáticos indios, chinos o persas, fue Pascal quien desarrolló muchas de sus aplicaciones y el primero en organizar la información de manera conjunta.
propiedades
- El Triángulo de Pascal es simétrico.
- La suma de todos los valores de la fila "n" es igual a 2n.
- Esto es así porque
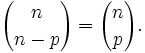 .
.
- Esto es debido a que, por el teorema del binomio, la expansión de la n-potencia de (1 + 1)n = 2n es
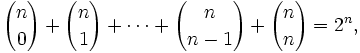
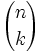 , de los términos del desarrollo del binomio de Newton.
, de los términos del desarrollo del binomio de Newton.