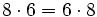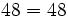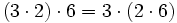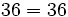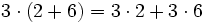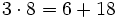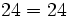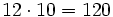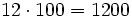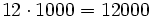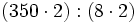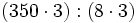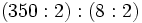Operaciones con números naturales (1º ESO)
De Wikipedia
| Revisión de 15:03 6 sep 2016 Coordinador (Discusión | contribuciones) (→Propiedades de la suma) ← Ir a diferencia anterior |
Revisión de 15:25 6 sep 2016 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 6: | Línea 6: | ||
| {{p}} | {{p}} | ||
| {{p}} | {{p}} | ||
| - | ==Suma y resta== | + | ==Suma de números naturales== |
| - | {{Caja Amarilla|texto=*'''Sumar''' es unir, juntar, añadir. | + | {{Caja Amarilla|texto='''Sumar''' es unir, juntar, añadir. |
| - | *'''Restar''' es quitar, hallar lo que falta o lo que sobra es decir , calcular la diferencia. | + | |
| }} | }} | ||
| {{p}} | {{p}} | ||
| Línea 37: | Línea 36: | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| - | Nota: La resta | ||
| {{AI_enlace | {{AI_enlace | ||
| |titulo1=Sumas | |titulo1=Sumas | ||
| |descripcion=Cálculo mental con sumas. | |descripcion=Cálculo mental con sumas. | ||
| |url1=http://maralboran.org/web_ma/Anaya/Anaya07/1ESO_ALUMNO/datos/01/03.htm | |url1=http://maralboran.org/web_ma/Anaya/Anaya07/1ESO_ALUMNO/datos/01/03.htm | ||
| + | }} | ||
| + | {{p}} | ||
| + | ==Resta de números naturales== | ||
| + | {{Caja Amarilla|texto='''Restar''' es quitar, hallar lo que falta o lo que sobra es decir , calcular la diferencia. | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| Línea 49: | Línea 51: | ||
| |url1=http://maralboran.org/web_ma/Anaya/Anaya07/1ESO_ALUMNO/datos/01/04.htm | |url1=http://maralboran.org/web_ma/Anaya/Anaya07/1ESO_ALUMNO/datos/01/04.htm | ||
| }} | }} | ||
| - | {{p}} | ||
| {{p}} | {{p}} | ||
| {{ejercicio | {{ejercicio | ||
| Línea 62: | Línea 63: | ||
| |sol= | |sol= | ||
| }} | }} | ||
| - | }} | ||
| - | |||
| - | ==Uso del Paréntesis== | ||
| - | {{Caja Amarilla|texto=En las expresiones con operaciones combinadas, los paréntesis empaquetan resultados y modifican el orden en que han de realizarse las operaciones. | ||
| - | }} | ||
| - | <br> | ||
| - | {{Ejemplo | ||
| - | |titulo=Ejemplo: ''Sumas y Restas con paréntesis y sin paréntesis'' | ||
| - | |enunciado= | ||
| - | :Jesús está mirando los últimos movimientos en su cuenta corriente. Tenía 2500 €; primero pago 450 € de gas, después pagó 325 € de luz y por último ingresó 1000 €. | ||
| - | |||
| - | :¿Cuánto dinero le queda a Jesús en su cuenta?. | ||
| - | |sol= | ||
| - | Se puede hacer de dos formas: | ||
| - | {{p}} | ||
| - | :a) 2500 - 450 - 325 + 1000 = 3500 - 775 = 2725 | ||
| - | :b) 2500 - ( 450 +325 )+ 1000 = 2500 -775 + 1000 = 2725 | ||
| - | {{p}} | ||
| - | En ambos casos la solución es 2725 €. | ||
| - | }} | ||
| - | <br> | ||
| - | {{ejercicio | ||
| - | |titulo=Ejercicio: ''Sumas y restas con paréntesis'' | ||
| - | |cuerpo= | ||
| - | {{ejercicio_cuerpo | ||
| - | |enunciado= | ||
| - | '''1.''' Calcula | ||
| - | {{p}} | ||
| - | :a) 52 - (25 - 13)= | ||
| - | :b) 40 - (32 - 16)= | ||
| - | :c) 28 + (11 - 6)= | ||
| - | :d) 37 + (15 - 12)= | ||
| - | {{p}} | ||
| - | |sol= | ||
| - | a) 40; b) 24; c) 33; d) 40}} | ||
| }} | }} | ||
| Línea 110: | Línea 76: | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| - | {{AI2|titulo=Actividad Interactiva: ''Multiplicación''|cuerpo= | + | {{AI_enlace |
| - | {{ai_cuerpo | + | |titulo1=Multiplicación 1 |
| - | |enunciado='''Actividad 1: '''Cálculo mental con multiplicaciones. | + | |descripcion=Cálculo mental con multiplicaciones. |
| - | |actividad= | + | |url1=http://maralboran.org/web_ma/Anaya/Anaya07/1ESO_ALUMNO/datos/01/05.htm |
| - | <center><iframe> | + | |
| - | url=http://maralboran.org/web_ma/Anaya/Anaya07/1ESO_ALUMNO/datos/01/05.htm | + | |
| - | width=800 | + | |
| - | height=650 | + | |
| - | name=myframe | + | |
| - | </iframe></center> | + | |
| - | <center>[http://maralboran.org/web_ma/Anaya/Anaya07/1ESO_ALUMNO/datos/01/05.htm '''Click''' aquí si no se ve bien la escena]</center> | + | |
| }} | }} | ||
| + | {{p}} | ||
| + | {{AI_enlace | ||
| + | |titulo1=Multiplicación 2 | ||
| + | |descripcion=Asocia los factores con su producto. | ||
| + | |url1=http://maralboran.org/web_ma/ciclo1/tabla.htm | ||
| }} | }} | ||
| - | <br> | ||
| - | {{ejercicio | ||
| - | |titulo=Ejercicio: ''la multiplicación'' | ||
| - | |cuerpo= | ||
| - | {{ejercicio_cuerpo | ||
| - | |enunciado= | ||
| - | '''1.''' Expresa como sumas de sumandos repetidos los siguientes productos | ||
| {{p}} | {{p}} | ||
| - | :a) 3 . 5 = | + | ==Propiedades de la multiplicación== |
| - | :b) 3 . 243 = | + | {{Teorema_sin_demo|titulo=Propiedades de la multiplicación|enunciado= |
| - | :c) 7 . 5 = | + | *'''Propiedad conmutativa''': El producto no varía al cambiar el orden de los factores. |
| {{p}} | {{p}} | ||
| - | |sol= | + | <center><math>a \cdot b = b \cdot a\,</math> </center>{{p}} |
| - | a) 3+3+3+3+3 ó 5+5+5 ; b) 3. 243 = 243 . 3 = 243 + 243 + 243; c) 7+7+7+7+7 ó 5+5+5+5+5+5+5;}} | + | *'''Propiedad asociativa''': El resultado de una multiplicación es independiente de la forma en que se agrupen los factores.{{p}} |
| + | <center><math>(a + b ) + c = a + ( b + c )\,</math></center> | ||
| + | *'''Propiedad distributiva''': El producto de un número por una suma (o resta) es igual a la suma (o rsta) de los productos del número por cada sumando.{{p}} | ||
| + | <center><math>a \cdot (b + c ) = a \cdot b + a \cdot \qquad a \cdot (b - c ) = a \cdot b - a \cdot c</math> </center> | ||
| }} | }} | ||
| - | <br> | ||
| {{p}} | {{p}} | ||
| - | {{AI2|titulo=Actividad Interactiva: ''Pregunta la tabla de multiplicar''|cuerpo= | + | {{Ejemplo_simple|titulo=Ejemplo:|contenido= |
| - | {{ai_cuerpo | + | |
| - | |enunciado='''Actividad 1: '''Asocia los factores con su producto | + | |
| - | |actividad= | + | |
| - | <center><iframe> | + | |
| - | url=http://maralboran.org/web_ma/ciclo1/tabla.htm | + | |
| - | width=700 | + | |
| - | height=550 | + | |
| - | name=myframe | + | |
| - | </iframe></center> | + | |
| - | <center>[http://maralboran.org/web_ma/ciclo1/tabla.htm '''Click''' aquí si no se ve bien la escena]</center> | + | |
| - | }} | + | |
| - | }} | + | |
| - | ==Propiedades de la multiplicación== | + | '''Conmutativa:''' |
| - | <center><table width="600" border="1"> | + | |
| - | <tr bgcolor="#CCCCCC"> | + | |
| - | <td width="295"><div align="center" class="Estilo5"><span class="Estilo3">Propiedad Conmutativa </span></div></td> | + | |
| - | <td width="289"><div align="center" class="Estilo5"><span class="Estilo3">Propiedad Asociativa</span></div></td> | + | |
| - | </tr> | + | |
| - | <tr> | + | |
| - | <td><div align="center"><span class="Estilo7">El producto no varía al cambiar el orden de los factores </span></div></td> | + | |
| - | <td><div align="center"><span class="Estilo7">El resultado de la multiplicación es independiente de la forma en que se agrupen los factores</span></div></td> | + | |
| - | </tr> | + | |
| - | <tr> | + | |
| - | <td><div align="center"> | + | |
| - | <p><strong><math>a \cdot b = b \cdot a</math> </strong></p> | + | |
| - | <p><strong><math>8 \cdot 6 = 6 \cdot 8</math> </strong></p> | + | |
| - | <p><strong><math>48\,</math> </strong></p> | + | |
| - | </div></td> | + | |
| - | <td><div align="center"> | + | |
| - | <p><strong><math>(a \cdot b ) \cdot c = a \cdot ( b \cdot c )</math> </strong></p> | + | |
| - | <p><strong><math>( 3 \cdot 2 ) \cdot 6 = 3 \cdot( 2 \cdot 6 )</math></strong></p> | + | |
| - | <p><strong><math>36\,</math></strong></p> | + | |
| - | </div></td> | + | |
| - | </tr> | + | |
| - | </table> | + | |
| - | </center> | + | |
| {{p}} | {{p}} | ||
| - | ===La distributiva del producto=== | + | <center><math>8 \cdot 6 = 6 \cdot 8\,</math></center> |
| - | {{Caja Amarilla|texto=El producto de un números por una suma (o resta ), es igual a la suma (o resta) de los productos parciales del número por cada sumando. | + | |
| - | + | ||
| - | *<math>a \cdot ( b + c ) = a \cdot b + a \cdot c</math> | + | |
| - | *<math>a \cdot ( b - c ) = a \cdot b - a \cdot c</math> | + | |
| - | }} | + | |
| {{p}} | {{p}} | ||
| - | {{Ejemplo_simple | + | <center><math>48 = 48\,</math></center> |
| - | |titulo=Ejemplo | + | {{p}} |
| - | |contenido= | + | '''Asociativa:''' |
| - | Podemos calcular {{sube|porcentaje=+15%|contenido=<math>100 \cdot 58 + 100 \cdot 12</math>}} de dos formas distintas: | + | |
| {{p}} | {{p}} | ||
| - | *'''Primera forma:''' | + | <center><math>( 3 \cdot 2 ) \cdot 6 = 3 \cdot ( 2 \cdot 6 )\,</math></center> |
| - | ::<math>100 \cdot 58 + 100 \cdot 12 = 5800 + 1200 = 7000</math> | + | {{p}} |
| - | *'''Segunda forma:''' | + | <center><math>6 \cdot 6 = 3 \cdot 12\,</math></center> |
| - | ::<math>100 \cdot 58 + 100 \cdot 12 = 100 \cdot (58 + 12) = 100 \cdot 70 = 7000</math> | + | {{p}} |
| + | <center><math>36 = 36\,</math></center> | ||
| + | {{p}} | ||
| + | '''Distributiva:''' | ||
| + | {{p}} | ||
| + | <center><math> 3 \cdot (2 + 6) = 3 \cdot 2 + 3 \cdot 6 \,</math></center> | ||
| + | {{p}} | ||
| + | <center><math>3 \cdot 8 = 6 + 18 \,</math></center> | ||
| + | {{p}} | ||
| + | <center><math>24 = 24\,</math></center> | ||
| + | |||
| }} | }} | ||
| {{p}} | {{p}} | ||
| Línea 203: | Línea 131: | ||
| |sol= | |sol= | ||
| Podemos resolver el problema de dos formas: | Podemos resolver el problema de dos formas: | ||
| + | |||
| *'''Primera forma:''' | *'''Primera forma:''' | ||
| + | |||
| ::Alfredo-----> <math>15 \cdot 4 = 60</math> | ::Alfredo-----> <math>15 \cdot 4 = 60</math> | ||
| ::Teresa------> <math>15 \cdot 2 = 30</math> | ::Teresa------> <math>15 \cdot 2 = 30</math> | ||
| - | ::Total---------> <math>(60 + 30)= 90\,</math> € | + | ::Total---------> <math>15 \cdot 4 + 15 \cdot 2 = 60 + 30= 90\,</math> € |
| + | |||
| *'''Segunda forma:''' | *'''Segunda forma:''' | ||
| - | ::Alfredo + Teresa compran 4 + 2 entradas | + | |
| + | ::Alfredo y Teresa compran 4 + 2 entradas | ||
| ::Luego en total gastan entre los dos: <math>15 \cdot (4 + 2 )= 15 \cdot 6 = 90</math> € | ::Luego en total gastan entre los dos: <math>15 \cdot (4 + 2 )= 15 \cdot 6 = 90</math> € | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| - | {{AI2|titulo=Actividad Interactiva: ''Propiedad Distributiva''|cuerpo= | + | {{AI_enlace |
| - | {{ai_cuerpo | + | |titulo1=Propiedad distributiva |
| - | |enunciado=:'''Actividad 1: '''Asocia las expresiones numéricas equivalentes | + | |descripcion=Asocia las expresiones numéricas equivalentes. |
| - | |actividad= | + | |url1=http://maralboran.org/web_ma/ciclo1/distributiva.htm |
| - | <center><iframe> | + | |
| - | url=http://maralboran.org/web_ma/ciclo1/distributiva.htm | + | |
| - | width=700 | + | |
| - | height=550 | + | |
| - | name=myframe | + | |
| - | </iframe></center> | + | |
| - | <center>[http://maralboran.org/web_ma/ciclo1/distributiva.htm '''Click''' aquí si no se ve bien la escena]</center> | + | |
| - | }} | + | |
| }} | }} | ||
| + | {{p}} | ||
| + | |||
| ===Producto por 10, 100, 1000, ....=== | ===Producto por 10, 100, 1000, ....=== | ||
| Línea 349: | Línea 275: | ||
| }} | }} | ||
| }} | }} | ||
| + | ==Uso del Paréntesis== | ||
| + | {{Caja Amarilla|texto=En las expresiones con operaciones combinadas, los paréntesis empaquetan resultados y modifican el orden en que han de realizarse las operaciones. | ||
| + | }} | ||
| + | <br> | ||
| + | {{Ejemplo | ||
| + | |titulo=Ejemplo: ''Sumas y Restas con paréntesis y sin paréntesis'' | ||
| + | |enunciado= | ||
| + | :Jesús está mirando los últimos movimientos en su cuenta corriente. Tenía 2500 €; primero pago 450 € de gas, después pagó 325 € de luz y por último ingresó 1000 €. | ||
| + | |||
| + | :¿Cuánto dinero le queda a Jesús en su cuenta?. | ||
| + | |sol= | ||
| + | Se puede hacer de dos formas: | ||
| + | {{p}} | ||
| + | :a) 2500 - 450 - 325 + 1000 = 3500 - 775 = 2725 | ||
| + | :b) 2500 - ( 450 +325 )+ 1000 = 2500 -775 + 1000 = 2725 | ||
| + | {{p}} | ||
| + | En ambos casos la solución es 2725 €. | ||
| + | }} | ||
| + | <br> | ||
| + | {{ejercicio | ||
| + | |titulo=Ejercicio: ''Sumas y restas con paréntesis'' | ||
| + | |cuerpo= | ||
| + | {{ejercicio_cuerpo | ||
| + | |enunciado= | ||
| + | '''1.''' Calcula | ||
| + | {{p}} | ||
| + | :a) 52 - (25 - 13)= | ||
| + | :b) 40 - (32 - 16)= | ||
| + | :c) 28 + (11 - 6)= | ||
| + | :d) 37 + (15 - 12)= | ||
| + | {{p}} | ||
| + | |sol= | ||
| + | a) 40; b) 24; c) 33; d) 40}} | ||
| + | }} | ||
| + | |||
| [[Categoría: Matemáticas]][[Categoría: Números]] | [[Categoría: Matemáticas]][[Categoría: Números]] | ||
Revisión de 15:25 6 sep 2016
| Enlaces internos | Para repasar | Para ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadora |
Tabla de contenidos |
Suma de números naturales
Sumar es unir, juntar, añadir.
Propiedades de la suma
Propiedades de la suma
- Propiedad conmutativa: La suma no varía al cambiar el orden de los sumandos.
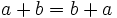
- Propiedad asociativa: El resultado de la suma es independiente de la forma en que se agrupen los sumandos.
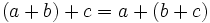
Cálculo mental con sumas.
Resta de números naturales
Restar es quitar, hallar lo que falta o lo que sobra es decir , calcular la diferencia.
Cálculo mental con restas.
|
Ejercicios propuestos: Sumas y restas |
Multiplicación o producto
Multiplicar, es una forma abreviada de realizar una suma de sumandos iguales.
Cálculo mental con multiplicaciones.
Asocia los factores con su producto.
Propiedades de la multiplicación
Propiedades de la multiplicación
- Propiedad conmutativa: El producto no varía al cambiar el orden de los factores.
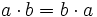
- Propiedad asociativa: El resultado de una multiplicación es independiente de la forma en que se agrupen los factores.
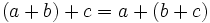
- Propiedad distributiva: El producto de un número por una suma (o resta) es igual a la suma (o rsta) de los productos del número por cada sumando.

Ejemplo: Propiedad distributiva del producto
- Alfredo va a comprar cuatro entradas para un concierto de rock y Teresa va a comprar dos entradas . ¿ Cuánto pagarán entre los dos si cada entrada cuesta 15 €?
Podemos resolver el problema de dos formas:
- Primera forma:
- Alfredo----->
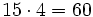
- Teresa------>
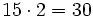
- Total--------->
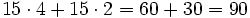 €
€
- Alfredo----->
- Segunda forma:
- Alfredo y Teresa compran 4 + 2 entradas
- Luego en total gastan entre los dos:
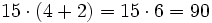 €
€
Asocia las expresiones numéricas equivalentes.
Producto por 10, 100, 1000, ....
Para multiplicar un número por la unidad seguida de ceros (10. 100, 1000,...), se añaden a la derecha del número tantos ceros como acompañan a la unidad (uno, dos , tres,...).
División
Dividir consiste en repartir en partes iguales o partir en partes de un determinado tamaño.
Una división puede ser exacta o entera dependiendo de su resto:
- Si el resto es 0 la división es exacta y el dividendo es igual al divisor por cociente:
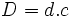
- Si el resto es distinto de cero la división es entera y el dividendo es igual al divisor por cociente mas el resto:
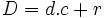
|
Actividad Interactiva: División
Actividad 1: Cálculo mental con divisiones.
Actividad 2: División entera.
|
Cociente por defecto y por exceso
Ejemplo: Cociente por defecto y por exceso
- Un autobús con 40 turistas sufre una avería camino de la estación . Como no hay tiempo, pues el tren no espera, el responsable del grupo decide acomodar a los viajeros en taxis de 4 plazas.
- a) ¿Cuántos taxis completarán?
- b) Supongamos ahora que fuesen 43 turistas . ¿ Cuántos taxis completarían ?.
- c) Y si nos preguntaran ¿cuántos taxis se necesitan?
- d) ¿cuál es el cociente por defecto y por exceso?
a) 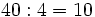 ---> completarán 10 taxis. (
---> completarán 10 taxis. (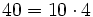 )
)
b) 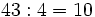 y sobrarían 3 turistas. (
y sobrarían 3 turistas. (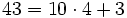 )
)
c) La respuesta sería 11, aunque en el último taxi quede un asiento libre.
Propiedades de la división
Alteraciones del cociente en una división
- Exacta: Si el dividendo y el divisor de una división exacta se multiplica o se divide por un mismo número distinto de cero, el cociente no varía.
- Entera: Si se multiplica o se divide el dividendo y el divisor por un mismo número distinto de cero, el cociente no varía pero el resto queda multiplicado o dividido por dicho número
Ejemplo: Propiedades de la división
- Observa la siguiente división exacta ,
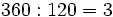 , y escribe los cocientes de las siguientes divisiones sin hacerlas:
, y escribe los cocientes de las siguientes divisiones sin hacerlas:
- a)
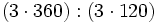
- b)

- c)

- a)
a) 3; b) 3; c) 3.
|
Ejercicio: Propiedades de la división
Solución: a) cociente=43 resto=12 b) cociente=43 resto=18 |
Orden en el que han de hacerse las operaciones
En las expresiones con operaciones combinadas, hemos de atender:
- 1º a los paréntesis.
- 2º a las multiplicaciones y a las divisiones.
- 3º a las sumas y a las restas.
|
Ejercicio: Prioridad en las operaciones 2. Calcula utilizando el orden de operaciones
Solución: a)28; b)244; c)64; d)76; e)76; f)304; |
Uso del Paréntesis
En las expresiones con operaciones combinadas, los paréntesis empaquetan resultados y modifican el orden en que han de realizarse las operaciones.
Ejemplo: Sumas y Restas con paréntesis y sin paréntesis
- Jesús está mirando los últimos movimientos en su cuenta corriente. Tenía 2500 €; primero pago 450 € de gas, después pagó 325 € de luz y por último ingresó 1000 €.
- ¿Cuánto dinero le queda a Jesús en su cuenta?.
Se puede hacer de dos formas:
- a) 2500 - 450 - 325 + 1000 = 3500 - 775 = 2725
- b) 2500 - ( 450 +325 )+ 1000 = 2500 -775 + 1000 = 2725
|
Ejercicio: Sumas y restas con paréntesis 1. Calcula
Solución: a) 40; b) 24; c) 33; d) 40 |
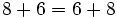
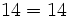
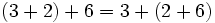
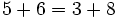
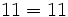
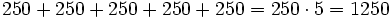 €
€