Plantilla:Sucesión de Fibonacci
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 12:53 8 sep 2016 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 13:02 8 sep 2016 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 2: | Línea 2: | ||
| |enunciado= | |enunciado= | ||
| [[Imagen:fibonacci.jpg|thumb|110px|[[Fibonacci]]]] | [[Imagen:fibonacci.jpg|thumb|110px|[[Fibonacci]]]] | ||
| - | :El siguiente problema fue propuesto por [[Fibonacci]], matemático italiano del siglo XIII: | + | {{b4}}El siguiente problema fue propuesto por [[Fibonacci]], matemático italiano del siglo XIII: |
| :"Cuántas parejas de conejos se producirán en un año, comenzando con una pareja única, si cada mes cualquier pareja engendra otra pareja, que se reproduce a su vez desde el segundo més?" | :"Cuántas parejas de conejos se producirán en un año, comenzando con una pareja única, si cada mes cualquier pareja engendra otra pareja, que se reproduce a su vez desde el segundo més?" | ||
Revisión de 13:02 8 sep 2016
Ejemplo: La sucesión de Fibonacci y el número áureo
El siguiente problema fue propuesto por Fibonacci, matemático italiano del siglo XIII:
- "Cuántas parejas de conejos se producirán en un año, comenzando con una pareja única, si cada mes cualquier pareja engendra otra pareja, que se reproduce a su vez desde el segundo més?"
- a) Escribe la sucesión cuyos términos son lás parejas de conejos que hay cada més. Esta recibe el nombre de sucesión de Fibonacci.
- b) Ahora vas a construir la sucesión que se obtiene al dividir cada término entre el anterior. Esa sucesión verás que se aproxima al número áureo (
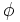 ):
):
Solución:
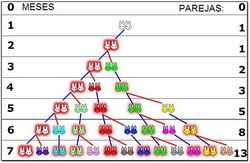
a) Sucesión de Fibonacci:
- Valor inicial: 1 pareja
- Mes 1: 1 pareja (hasta el segundo mes no se reproduce la primera)
- Mes 2: 2 parejas (primera vez que se reproduce)
- Mes 3: 3 parejas (la primera pareja vuelve a reproducirse pero la segunda no lo hace hasta el próximo mes)
- Mes 4: 5 parejas (la primera y la segunda pareja ya se reproducen, la tercera aún no)
- Mes 5: 8 parejas (se reproducen las 3 primeras parejas, las otras dos no)
- Mes 6: 13 parejas (se reproducen las 5 parejas de hace 2 meses, pero las 3 nuevas del mes anterior aún no)
Así se obtiene una sucesión en la que cada término se obtiene a partir de la suma de los dos anteriores:
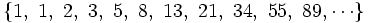
b) Sucesión del número áureo:
Dividiendo cada término entre el anterior, tenemos la sucesión:
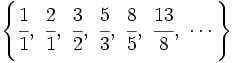
que expresada con decimales vemos que se aproxima al número áureo:
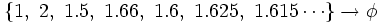
Nota: Leonardo de Pisa (Fibonacci), en su Libro de los ábacos (Liber abacci, 1202, 1228), usa la sucesión que lleva su nombre para calcular el número de pares de conejos n meses después de que una primera pareja comienza a reproducirse (suponiendo que los conejos están aislados por muros, se empiezan a reproducir cuando tienen dos meses de edad, tardan un mes desde la fecundación hasta la parición y cada camada es de dos conejos). Este es un problema matemático puramente independiente de que sean conejos los involucrados. En realidad, el conejo común europeo tiene camadas de 4 a 12 individuos y varias veces al año, aunque no cada mes, pese a que la preñez dura 32 días. El problema se halla en las páginas 123 y 124 del manuscrito de 1228, que fue el que llegó hasta nosotros, y parece que el planteamiento recurrió a conejos como pudiera haber sido a otros seres; es un soporte para hacer comprensible una incógnita, un acertijo matemático.