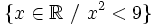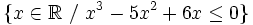Plantilla:Intervalos y semirrectas
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 11:46 9 sep 2016 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 12:20 9 sep 2016 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 53: | Línea 53: | ||
| <br> | <br> | ||
| <br> | <br> | ||
| - | b) <math>\left [ 2, 5 \right )</math> | + | b) <math>[ 2, 5 )\;</math> |
| <br> | <br> | ||
| <br> | <br> | ||
| <br> | <br> | ||
| <br> | <br> | ||
| - | c) <math>\left [ 3, 7 \right ]</math> | + | c) <math>[ 3, 7 ]\;</math> |
| <br> | <br> | ||
| <br> | <br> | ||
| <br> | <br> | ||
| <br> | <br> | ||
| - | d) <math>\left ( -\infty, 1 \right ) - \left \{ 0 \right \}</math> | + | d) <math> ( -\infty, 1 ) - \left \{ 0 \right \} = (-\infty, 0) \cup (0,1)</math> |
| <br> | <br> | ||
| <br> | <br> | ||
| <br> | <br> | ||
| <br> | <br> | ||
| - | e) <math>\left ( -\infty, -2 \right ] \cup \left [ 2 , +\infty \right ]</math> | + | e) <math>( -\infty, -2 ] \cup [ 2 , +\infty ]</math> |
| |celda2=<center>[[Imagen:ER29_1.png|left]]</center>}} | |celda2=<center>[[Imagen:ER29_1.png|left]]</center>}} | ||
| }} | }} | ||
Revisión de 12:20 9 sep 2016
Para designar algunos tramos de la recta real, existe una nomenclatura que debes conocer:
La recta real se representa en forma de intervalo: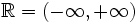
|
En este vídeo introducimos los conceptos de intervalo abierto (a;b), intervalo cerrado [a;b], intervalo abierto por la izquierda y cerrado por la derecha (a;b], intervalo cerrado por la izquierda y abierto por la derecha [a;b). También hablamos de la amplitud de un intervalo y de los intervalos de amplitud infinita, llamados "no acotados".
Ejercicios resueltos: Intervalos y semirrectas
- 1. Representar los siguientes conjuntos numéricos:
- a) Números mayores que 3.
- b)
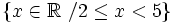
- b)
- c)
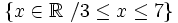
- c)
- d) Números menores que 1 excluyendo el 0.
- e)
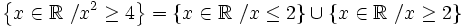
- e)
|
Actividad: Intervalos y semirrectas
Solución: Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones:
|
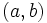
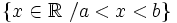
![[a, b]\,\!](/wikipedia/images/math/8/b/5/8b596d04e319e05cadcc7dcf251a9815.png)
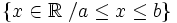
![(a, b]\,\!](/wikipedia/images/math/e/4/5/e4598ac5b1b1c763827cd6adf382190b.png)
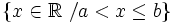
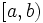
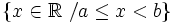
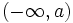
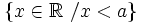
![( - \infty , a]\,\!](/wikipedia/images/math/a/5/3/a537d0975ab601b18b2e6f48b6700575.png)
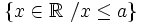
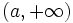
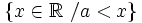
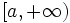
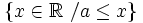
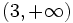
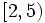
![[ 3, 7 ]\;](/wikipedia/images/math/5/2/5/525d3facf3fc1d833da47b47559cbd4a.png)
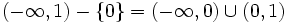
![( -\infty, -2 ] \cup [ 2 , +\infty ]](/wikipedia/images/math/8/7/c/87c992202512c1d40eb658f6c4171c9a.png)

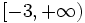
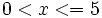
![(-\infty,7],\ [-8,9),\ [-4,7] \;](/wikipedia/images/math/6/f/c/6fcf1a640e06f181cdd7f64424e1953a.png)