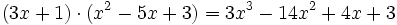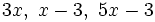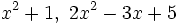Plantilla:Divisibilidad de polinomios
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 16:30 9 sep 2016 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 16:30 9 sep 2016 Coordinador (Discusión | contribuciones) (→Polinomios irreducibles) Ir a siguiente diferencia → |
||
| Línea 23: | Línea 23: | ||
| {{Caja_Amarilla|texto=Un polinomio <math>P(x)\,</math> es '''irreducible''' cuando ningún polinomio de grado inferior es divisor suyo.}} | {{Caja_Amarilla|texto=Un polinomio <math>P(x)\,</math> es '''irreducible''' cuando ningún polinomio de grado inferior es divisor suyo.}} | ||
| {{p}} | {{p}} | ||
| - | {{Desplegable|titulo=Ejemplos:{{b}}|contenido= | + | {{Ejemplo_simple|titulo=Ejemplos|contenido= |
| Son polinomios irreducibles, entre otros: | Son polinomios irreducibles, entre otros: | ||
| * Los de primer grado: <math>3x,\ x-3,\ 5x-3\ \;</math> | * Los de primer grado: <math>3x,\ x-3,\ 5x-3\ \;</math> | ||
| * Los de segundo grado sin raíces: <math>x^2+1,\ 2x^2-3x+5 \;</math> | * Los de segundo grado sin raíces: <math>x^2+1,\ 2x^2-3x+5 \;</math> | ||
| }} | }} | ||
Revisión de 16:30 9 sep 2016
Polinomios múltiplos y divisores
Un polinomio  es divisor de otro,
es divisor de otro,  y lo representaremos por
y lo representaremos por 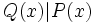 , si la división
, si la división 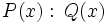 es exacta, es decir, cuando existe otro polinomio
es exacta, es decir, cuando existe otro polinomio 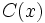 tal que:
tal que:
|
|
También diremos que  es divisible por
es divisible por  o que
o que  es un múltiplo de
es un múltiplo de  .
.
La divisibilidad de polinomios es semejante a la divisibilidad con números enteros. Asimismo, la factorización de polinomios equivale a la descomposición de un número en factores primos, y los conceptos de máximo común divisor, mínimo común múltiplo e irreducibilidad son similares a los correspondientes conceptos numéricos.
Polinomios irreducibles
Un polinomio  es irreducible cuando ningún polinomio de grado inferior es divisor suyo.
es irreducible cuando ningún polinomio de grado inferior es divisor suyo.
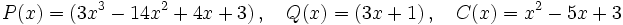 :
:
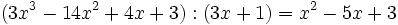 , porque
, porque