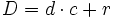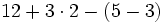Operaciones con números naturales (1º ESO)
De Wikipedia
| Revisión de 02:44 10 sep 2016 Coordinador (Discusión | contribuciones) (→Resta) ← Ir a diferencia anterior |
Revisión de 02:45 10 sep 2016 Coordinador (Discusión | contribuciones) (→Multiplicación o producto) Ir a siguiente diferencia → |
||
| Línea 94: | Línea 94: | ||
| |titulo1=Cálculo mental con multiplicaciones | |titulo1=Cálculo mental con multiplicaciones | ||
| |descripcion=Cálculo mental con multiplicaciones. | |descripcion=Cálculo mental con multiplicaciones. | ||
| + | <center><iframe> | ||
| + | url=http://maralboran.org/web_ma/Anaya/Anaya07/1ESO_ALUMNO/datos/01/05.htm | ||
| + | width=800 | ||
| + | height=650 | ||
| + | name=myframe | ||
| + | </iframe></center> | ||
| + | |||
| |url1=http://maralboran.org/web_ma/Anaya/Anaya07/1ESO_ALUMNO/datos/01/05.htm | |url1=http://maralboran.org/web_ma/Anaya/Anaya07/1ESO_ALUMNO/datos/01/05.htm | ||
| }} | }} | ||
| Línea 99: | Línea 106: | ||
| {{AI_enlace | {{AI_enlace | ||
| |titulo1=Asocia los factores con su producto | |titulo1=Asocia los factores con su producto | ||
| - | |descripcion=. | + | |descripcion= |
| + | |||
| + | <center><iframe> | ||
| + | url=http://maralboran.org/web_ma/ciclo1/tabla.htm | ||
| + | width=800 | ||
| + | height=650 | ||
| + | name=myframe | ||
| + | </iframe></center> | ||
| |url1=http://maralboran.org/web_ma/ciclo1/tabla.htm | |url1=http://maralboran.org/web_ma/ciclo1/tabla.htm | ||
| }} | }} | ||
| Línea 188: | Línea 202: | ||
| }} | }} | ||
| (Pág. 14-15) | (Pág. 14-15) | ||
| + | |||
| ==División== | ==División== | ||
| Dividir consiste en repartir una cantidad en partes iguales o partir en partes de un determinado tamaño. Mas concretamente: | Dividir consiste en repartir una cantidad en partes iguales o partir en partes de un determinado tamaño. Mas concretamente: | ||
Revisión de 02:45 10 sep 2016
| Enlaces internos | Para repasar | Para ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadora |
Tabla de contenidos |
(Pág. 12)
Suma y resta de números naturales
Suma
Sumar es unir, juntar, añadir.
Propiedades de la suma
Propiedades de la suma
- Propiedad conmutativa: La suma no varía al cambiar el orden de los sumandos.
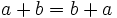
- Propiedad asociativa: El resultado de la suma es independiente de la forma en que se agrupen los sumandos.
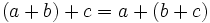
Cálculo mental con sumas.
Resta
Restar es quitar, hallar lo que falta o lo que sobra, es decir, calcular la diferencia.
Cálculo mental con restas.
Ejercicios propuestos
|
Ejercicios propuestos: Sumas y restas |
(Pág. 13)
Multiplicación o producto
Multiplicar, es una forma abreviada de realizar una suma de sumandos iguales.
Cálculo mental con multiplicaciones.
Propiedades de la multiplicación
Propiedades de la multiplicación
- Propiedad conmutativa: El producto no varía al cambiar el orden de los factores.
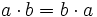
- Propiedad asociativa: El resultado de una multiplicación es independiente de la forma en que se agrupen los factores.
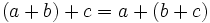
- Propiedad distributiva: El producto de un número por una suma (o resta) es igual a la suma (o rsta) de los productos del número por cada sumando.

Ejemplo: Propiedad distributiva del producto
- Alfredo va a comprar cuatro entradas para un concierto de rock y Teresa va a comprar dos entradas . ¿ Cuánto pagarán entre los dos si cada entrada cuesta 15 €?
Podemos resolver el problema de dos formas:
- Primera forma:
- Alfredo----->
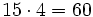
- Teresa------>
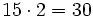
- Total--------->
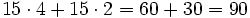 €
€
- Alfredo----->
- Segunda forma:
- Alfredo y Teresa compran 4 + 2 entradas
- Luego en total gastan entre los dos:
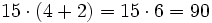 €
€
Asocia las expresiones numéricas equivalentes.
Producto por 10, 100, 1000, ....
Para multiplicar un número por la unidad seguida de ceros (10, 100, 1000,...), se añaden a la derecha del número tantos ceros como acompañan a la unidad (uno, dos , tres,...).
Ejercicios propuestos
|
Ejercicios propuestos: Multiplicación |
(Pág. 14-15)
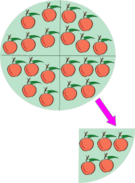
División
Dividir consiste en repartir una cantidad en partes iguales o partir en partes de un determinado tamaño. Mas concretamente:
Sean
|
Algoritmo de la división
Dados  y
y  , dos números naturales cualesquiera, existen dos únicos números naturales,
, dos números naturales cualesquiera, existen dos únicos números naturales,  y
y  , tales que:
, tales que:
|
|
 es el dividendo,
es el dividendo,  el divisor,
el divisor,  el cociente y
el cociente y  el resto.
el resto.
Ver demostración en Wikipedia
Cálculo mental con divisiones.
Cálculo con divisiones.
|
Actividad: Cociente y resto
Solución: Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones:
|
Cociente por defecto y por exceso
Ejemplo: Cociente por defecto y por exceso
- Un autobús con 43 turistas sufre una avería camino de la estación . Como no hay tiempo, pues el tren no espera, el responsable del grupo decide acomodar a los viajeros en taxis de 4 plazas.
- a) ¿Cuántos taxis completarán?
- b) ¿Cuántos taxis se necesitan?
- c) ¿cuál es el cociente por defecto y por exceso?
a) Completan 10 taxis y sobran 3 turistas. (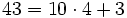 )
)
b) Se necesitan 11 taxis, aunque en el último taxi quede un asiento libre.
Propiedades de la división
Propiedad
- Si se multiplica o se divide el dividendo y el divisor por un mismo número distinto de cero, el cociente no varía pero el resto queda multiplicado o dividido por dicho número.
- Hagamos la división
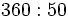
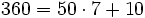 (Cociente=7; Resto=10)
(Cociente=7; Resto=10)- Ahora dividimos el dividendo y el divisor por 10:
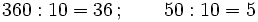
- y volvemos a hacer la división:
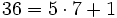 (Cociente=7; Resto=1)
(Cociente=7; Resto=1)- Es decir, el cociente no varía y el resto queda dividido por 10.
Ejercicios propuestos
|
Ejercicios propuestos: División |
(Pág. 16-17)
Operaciones combinadas
Jerarquía de las operaciones
- Primero se efectúan las operaciones del interior de los paréntesis. Si hay paréntesis anidados, se efectúan de dentro hacia fuera.
- Dentro de los paréntesis, o una vez quitados todos los paréntesis, las operaciones se efectúan en el siguiente orden:
- Las multiplicaciones y las divisiones.
- Las sumas y las restas.
- Efectúa las siguientes operaciones combinadas:
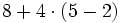
- Solución:
- Los paréntesis
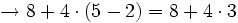
- Las multiplicaciones y divisiones
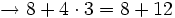
- Las sumas y restas
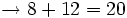
Ejercicios propuestos
|
Ejercicios propuestos: División |
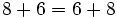
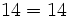
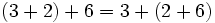
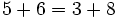
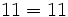
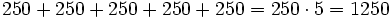 €
€
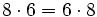
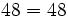
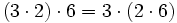

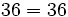
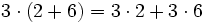
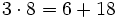
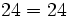
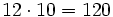
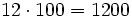
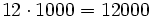
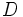 y
y 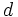 dos números naturales, con
dos números naturales, con 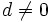 .
.
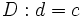
 , cociente.
, cociente.
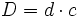 ), diremos que la división es exacta.
), diremos que la división es exacta.
 , menor que
, menor que 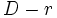 entre
entre