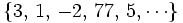Plantilla:Sucesión de números reales
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 23:10 13 sep 2016 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 23:32 13 sep 2016 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 15: | Línea 15: | ||
| Los términos de una sucesión pueden seguir un cierto criterio: | Los términos de una sucesión pueden seguir un cierto criterio: | ||
| - | *<math>\{ 2, 5, 8, 11, 14, 17, \cdots \}</math>. Sus términos se obtienen sumando 3 al anterior. | + | *<math>\{ 2, \, 5, \, 8, \, 11, \, 14, \, 17, \cdots \}</math>. Sus términos se obtienen sumando 3 al anterior. |
| - | *<math>\{ 1, 2, 4, 8, 16, 32, \cdots \}</math>. Sus términos son las potencias de 2. | + | *<math>\{ 1, \, 2, \, 4, \, 8, \, 16, \, 32, \cdots \}</math>. Sus términos son las potencias de 2. |
| - | *<math>\{ 1, -1, 2, -2, 3, -3, \cdots \}</math>. Sus términos van ascendiendo y alternando el signo. | + | *<math>\{ 1, \, -1, \, 2, \, -2, \, 3, \, -3, \cdots \}</math>. Sus términos van ascendiendo y alternando el signo. |
| - | *<math>\{ 2, 3, 5, 8, 13, 21, \cdots \}</math>. Sus términos, a partir del tercero, se obtienen sumando los dos anteriores. | + | *<math>\{ 2, \, 3, \, 5, \, 8, \, 13, \, 21, \cdots \}</math>. Sus términos, a partir del tercero, se obtienen sumando los dos anteriores. |
| o no seguir ninguno: | o no seguir ninguno: | ||
| - | *<math>\{ 3, 1, -2, 77, 5, \cdots \}</math> | + | *<math>\{ 3, \, 1, \, -2, \, 77, \, 5, \cdots \}</math> |
| }} | }} | ||
| {{p}} | {{p}} | ||
Revisión de 23:32 13 sep 2016
Una sucesión de números reales es una función 
, que a cada número natural 
le asocia un número real 
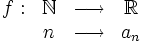
Esto genera el conjunto ordenado
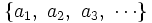
que se llaman los términos de la sucesión.
Se suele identificar a la sucesión con sus términos. Normalmente hablaremos de la sucesión de términos 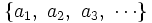en lugar de la sucesión .
Los términos de una sucesión pueden seguir un cierto criterio:
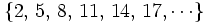. Sus términos se obtienen sumando 3 al anterior.
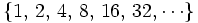. Sus términos son las potencias de 2.
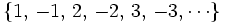. Sus términos van ascendiendo y alternando el signo.
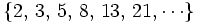. Sus términos, a partir del tercero, se obtienen sumando los dos anteriores.
o no seguir ninguno:
Función o aplicación entre conjuntos (6´25") Sinopsis: El concepto de función o aplicación ente dos conjuntos es necesario para la definición de sucesión.
