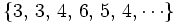Plantilla:Sucesión de números reales
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 23:35 13 sep 2016 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 09:42 14 sep 2016 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 1: | Línea 1: | ||
| - | {{Caja_Amarilla|texto=Una '''sucesión''' de números reales es una función <math>f \;</math>, que a cada número natural <math>n \;</math> le asocia un número real <math>a_n \;</math> | + | {{Caja_Amarilla|texto=Una '''sucesión''' de números reales es una función <math>f \;</math>, que a cada número natural <math>n \;</math> le asocia un único número real <math>a_n \;</math> |
| <center><math>\begin{matrix}f: & \mathbb{N} & \longrightarrow & \mathbb{R} \\ \ & n & \longrightarrow & a_n \end{matrix}</math></center> | <center><math>\begin{matrix}f: & \mathbb{N} & \longrightarrow & \mathbb{R} \\ \ & n & \longrightarrow & a_n \end{matrix}</math></center> | ||
| Línea 5: | Línea 5: | ||
| Esto genera el conjunto ordenado | Esto genera el conjunto ordenado | ||
| - | <center><math>\{ a_1,\ a_2,\ a_3,\ \cdots \}</math></center> | + | <center><math>\{ a_1,\ a_2,\ a_3,\ \cdots \ , a_n,\ \cdots}</math></center> |
| que se llaman los '''términos''' de la sucesión. | que se llaman los '''términos''' de la sucesión. | ||
Revisión de 09:42 14 sep 2016
Una sucesión de números reales es una función 
, que a cada número natural 
le asocia un único número real 
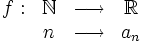
Esto genera el conjunto ordenado
que se llaman los términos de la sucesión.
Se suele identificar a la sucesión con sus términos. Normalmente hablaremos de la sucesión de términos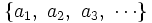 
en lugar de la sucesión .
Los términos de una sucesión pueden seguir un cierto criterio:
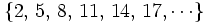. Sus términos se obtienen sumando 3 al anterior.
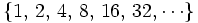. Sus términos son las potencias de 2.
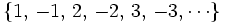. Sus términos van ascendiendo y alternando el signo.
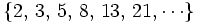. Sus términos, a partir del tercero, se obtienen sumando los dos anteriores.
o no seguir ninguno:
Función o aplicación entre conjuntos (6´25") Sinopsis: El concepto de función o aplicación ente dos conjuntos es necesario para la definición de sucesión.
