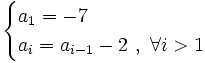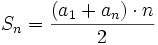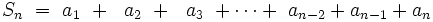Plantilla:Progresiones aritméticas
De Wikipedia
| Revisión de 16:02 14 sep 2016 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 16:04 14 sep 2016 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 2: | Línea 2: | ||
| {{p}} | {{p}} | ||
| ===Término general de una progresión aritmética=== | ===Término general de una progresión aritmética=== | ||
| - | {{Teorema | + | {{Término general de una progresión aritmética}} |
| - | |titulo=''Término general de una progresión aritmética'' | + | |
| - | |enunciado= | + | |
| - | :Sean <math>a_1, a_2, a_3, ..... \;\!</math>términos de una progresión aritmética de diferencia <math>d\;\!</math>. Entonces, se cumple que:{{p}} | + | |
| - | {{Caja|contenido= | + | |
| - | <math>a_n = a_1 + (n - 1) \cdot d \;\!</math> | + | |
| - | }} | + | |
| - | |demo= | + | |
| - | En efecto, de forma intuitiva: | + | |
| - | <center><math>a_1 = a_1 + 0 \cdot d \;\!</math></center> | + | |
| - | + | ||
| - | <center><math>a_2 = a_1 + d = a_1 + 1 \cdot d \;\!</math> | + | |
| - | + | ||
| - | <math>a_3 = a_2 + d = a_1 + d + d = a_1 + 2 \cdot d \;\!</math> | + | |
| - | + | ||
| - | <math>a_4 = a_3 + d = a_1 +2d + d = a_1 + 3 \cdot d \;\!</math> | + | |
| - | + | ||
| - | ........................ | + | |
| - | + | ||
| - | <math>a_n = a_1 + (n - 1) \cdot d \;\!</math> | + | |
| - | </center> | + | |
| - | --------------- | + | |
| - | '''Demostración por el método de inducción completa:''' | + | |
| - | + | ||
| - | Para ello hay que comprobar primero que la fórmula se cumple para n=1. A continuación, suponiendo que la fórmula es cierta para el valor n, deberemos comprobar que también se cumple para el valor n+1. Con ésto, la fórmula será cierta para todo valor n natural. | + | |
| - | + | ||
| - | Veamos que se cumple para n=1. Sustituimos n por 1 en el lado derecho de la fórmula: | + | |
| - | + | ||
| - | <center><math>a_1+(1-1) \cdot d = a_1 + 0 \cdot d = a_1</math></center> | + | |
| - | + | ||
| - | con lo que queda comprobada para n=1. | + | |
| - | + | ||
| - | Supongamos que la fórmula es cierta para el valor n: | + | |
| - | + | ||
| - | <center><math>a_n=a_1+(n-1) \cdot d</math>.{{b4}}[1]</center> | + | |
| - | + | ||
| - | Por ser una progresión aritmética cada término se obtiene sumando d al anterior término: | + | |
| - | + | ||
| - | <center><math>a_{n+1}= a_n+ d \;</math>{{b4}}[2]</center> | + | |
| - | + | ||
| - | Debemos comprobar que se cumple para el valor n+1: | + | |
| - | + | ||
| - | <center><math>a_{n+1}\begin{matrix} ~_{[2]}~ \\ = \\ ~ \end{matrix}a_n+ d \begin{matrix} ~_{[1]}~ \\ = \\ ~ \end{matrix} a_1 + (n-1) \cdot d + d =a_1 + ((n+1)-1) \cdot d</math></center> | + | |
| - | + | ||
| {{p}} | {{p}} | ||
| - | Verificando así que la fórmula se cumple para el valor n+1 y terminando la demostración por inducción. | ||
| - | |||
| - | |||
| - | }} | ||
| - | {{p}} | ||
| - | {{Video_enlace | ||
| - | |titulo1=Progresión aritmética | ||
| - | |duracion=10´21" | ||
| - | |url1=http://matematicasbachiller.com/videos/1-bachillerato/matematicas-de-primero-de-bachillerato/04-sucesiones-aritmeticas-sucesiones-geometricas/03-sucesion-aritmetica#.VCaipPl_u2E | ||
| - | |sinopsis=*Definición de progresión aritmética. | ||
| - | *Ejemplos | ||
| - | *Término general | ||
| - | }} | ||
| - | {{p}} | ||
| - | |||
| ===Suma de términos de una progresión aritmética=== | ===Suma de términos de una progresión aritmética=== | ||
| {{Teorema | {{Teorema | ||
Revisión de 16:04 14 sep 2016
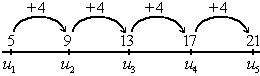
Una progresión aritmética es una sucesión de números en la que cada término se obtiene sumando al anterior una cantidad fija,  , que llamaremos diferencia.
, que llamaremos diferencia.
Escrito en forma recursiva:
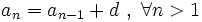
Por ejemplo, la sucesión 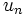 :
:
es una progresión aritmética con diferencia 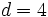 .
.
Progresiones aritméticas: definición y ejemplos.
Determina el quinto término de la siguiente progresión aritmética: {-3, -7, -11, -15, ...}
Dados los términos de una progresión aritmética, completar la fórmula de recurrencia.
Actividades en las que aprenderás el concepto de progresión aritmética y a cómo identificarlas.
Actividades de introducción a las sucesiones aritméticas.
Fórmulas recursivas para sucesiones aritméticas.
Extiende sucesiones aritméticas.
Fórmulas recursivas para sucesiones aritméticas.
Término general de una progresión aritmética
Término general de una progresión aritmética
El término general, 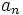 , de una progresión aritmética de diferencia
, de una progresión aritmética de diferencia  es:
es:
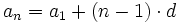
En efecto, de forma intuitiva:
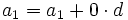
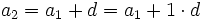
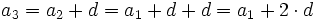
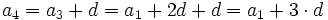
........................
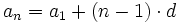
Demostración por el método de inducción completa:
Para ello hay que comprobar primero que la fórmula se cumple para n=1. A continuación, suponiendo que la fórmula es cierta para el valor n, deberemos comprobar que también se cumple para el valor n+1. Con ésto, la fórmula será cierta para todo valor n natural.
Veamos que se cumple para n=1. Sustituimos n por 1 en el lado derecho de la fórmula:
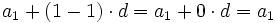
con lo que queda comprobada para n=1.
Supongamos que la fórmula es cierta para el valor n:
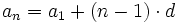 . [1]
. [1]Por ser una progresión aritmética cada término se obtiene sumando d al anterior término:
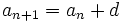 [2]
[2]Debemos comprobar que se cumple para el valor n+1:
![a_{n+1}\begin{matrix} ~_{[2]}~ \\ = \\ ~ \end{matrix}a_n+ d \begin{matrix} ~_{[1]}~ \\ = \\ ~ \end{matrix} a_1 + (n-1) \cdot d + d =a_1 + ((n+1)-1) \cdot d](/wikipedia/images/math/7/4/4/744cf81c67660fb80f54db415de019dd.png)
- Definición de progresión aritmética.
- Término general
- Ejemplos
Tutorial en el que se explica y trabajan las progresiones aritméticas, la ley de recurrencia y el término general que las genera, así como alguna de sus propiedades básicas.
Término general de una progresión aritmética: Obtención y ejemplos.
Término general de una progresión aritmética: Más ejemplos
Término general de una progresión aritmética a partir de términos intermedios.
- Definición de progresión aritmética.
- Ejemplos
- Término general
- Una progresión aritmética tiene como término general
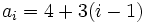 , halla el término
, halla el término 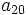 .
.
- Halla el término
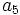 de una progresión aritmética que viene dada por la siguiente ley de recurrencia:
de una progresión aritmética que viene dada por la siguiente ley de recurrencia:
Halla el término general y la forma recursiva de las siguientes progresiones aritméticas:
- a) {-5, -3, -1, 1, ...}
- b) {100, 107, 114, 121, ...}
- c) {1, 3, 6, 10, ...}
Halla el término general de las siguientes progresiones aritméticas:
- a) {12, 5, -2, -9, ...}
- b) {-100, -50, 0, 50, ...}
Halla el término 100 de la siguiente progresión aritmética: {15, 9, 3, -3, ...}.
Halla la forma recursiva de la progresión aritmética con término general 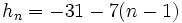
Actividad de introducción a las fórmulas de sucesiones aritméticas.
Actividad para aprender a obtener el término general (fórmula explícita) de sucesiones aritméticas.
Actividades en las que aprenderás a obtener el término general de una progresión aritmética.
Convertir formas de sucesiones aritméticas, recursivas y explícitas.
Repaso de sucesiones aritméticas.
Usa el término general de progresiones aritméticas.
Obtén el término general (fórmula explícita) de sucesiones aritméticas.
Encuentra el término general de una progresión aritmética dada.
Convertir formas de sucesiones aritméticas, recursivas y explícitas.
Suma de términos de una progresión aritmética
Suma de términos de una progresión aritmética
- La suma de los n primeros términos de una progresión aritmética es:
|
|
El porqué de esta fórmula se deduce de la siguiente historia:
- En un pequeño pueblo de Alemania, Brunswick, un día en la escuela el profesor manda sumar los cien primeros números naturales. El maestro quería unos minutos de tranquilidad... pero transcurridos pocos segundos uno de los alumnos levanta la mano y dice tener la solución: los cien primeros números naturales suman 5.050. Y efectivamente, así era.
- El profesor le preguntó ¿cómo lo has hecho? El niño le dijo: 1 + 100 = 101, 2 + 99 = 101, 3 + 98 = 101,... siempre suma 101 y hay 50 sumas, en total 50 * 101 = 5050. El profesor quedó tan impresionado que le regaló un libro de Aritmética.
- Ese niño tenía 10 años y se llamaba Carl Friedrich Gaüss. Fue uno de los mas grandes matemáticos. Intenta enterarte de algo más sobre él.
Demostración:
Para la demostración nos basaremos en el hecho de que:
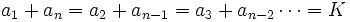
Entonces, si efectuamos la siguiente suma:
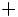
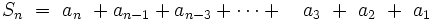
- _______________________________________________________________
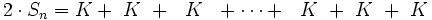
por tanto:
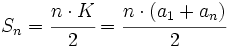
Demostración de la fórmula de la suma de los n primeros términos de una progresión aritmética