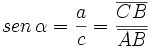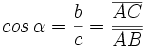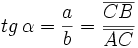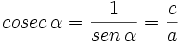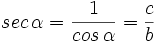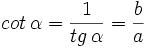Razones trigonométricas de un ángulo agudo (1ºBach)
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 19:28 15 sep 2016 Coordinador (Discusión | contribuciones) (→Calculadora) ← Ir a diferencia anterior |
Revisión de 15:33 17 sep 2016 Coordinador (Discusión | contribuciones) (→Razones trigonométricas de algunos ángulos importantes) Ir a siguiente diferencia → |
||
| Línea 200: | Línea 200: | ||
| |duracion=4´54" | |duracion=4´54" | ||
| |url1=http://matematicasbachiller.com/videos/1-bachillerato/matematicas-de-primero-de-bachillerato/05-angulos-agudos/04-razones-trigonometricas-de-angulos-complementarios#.VCfDrPl_u2E | |url1=http://matematicasbachiller.com/videos/1-bachillerato/matematicas-de-primero-de-bachillerato/05-angulos-agudos/04-razones-trigonometricas-de-angulos-complementarios#.VCfDrPl_u2E | ||
| - | |sinopsis=Videotutorial | + | |sinopsis=*Dos ángulos agudos se dicen complementarios si suman 90º. |
| + | *El seno de un ángulo agudo coincide con el coseno de su complementario. | ||
| + | *La tangente de un ángulo agudo coincide con la cotangente de su complementario. | ||
| + | *La secante de un ángulo agudo coincide con la cesecante de su complementario. | ||
| + | |||
| }} | }} | ||
| {{p}} | {{p}} | ||
| Línea 207: | Línea 211: | ||
| |duracion=6´59" | |duracion=6´59" | ||
| |url1=http://matematicasbachiller.com/videos/1-bachillerato/matematicas-de-primero-de-bachillerato/05-angulos-agudos/05-razones-trigonometricas-de-los-angulos-mas-famosos#.VCfETfl_u2E | |url1=http://matematicasbachiller.com/videos/1-bachillerato/matematicas-de-primero-de-bachillerato/05-angulos-agudos/05-razones-trigonometricas-de-los-angulos-mas-famosos#.VCfETfl_u2E | ||
| - | |sinopsis=Videotutorial | + | |sinopsis=*Apoyándonos en un triángulo equilátero de lado unidad, en este vídeo determinamos las razones trigonométricas de los ángulos de 30º y 60º. |
| + | *También determinamos las razones trigonométricas del ángulo de 45º; para ello nos servimos de un triángulo rectángulo de catetos unitarios. | ||
| + | *Las razones trigonométricas en cuestión deben memorizarse. | ||
| + | |||
| }} | }} | ||
| {{p}} | {{p}} | ||
Revisión de 15:33 17 sep 2016
Menú:
| Enlaces internos | Para repasar o ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadoras |
Tabla de contenidos |
(Pág. 106)
Razones trigonométricas de un ángulo agudo
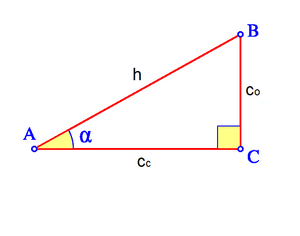
Dado un triángulo rectángulo ABC, se definen las razones trigonométricas del ángulo agudo  , de la siguiente manera:
, de la siguiente manera:
|
Razones trigonométricas inversas
Las razones trigonométricas inversas se definen de la siguiente manera:
- La cosecante (abreviado como csc o cosec), razón inversa del seno:
- La secante (abreviado como sec), razón inversa del coseno:
- La cotangente (abreviado como cot), razón inversa de la tangente:
- Razones trigonométricas de un ángulo agudo.
- Razones trigonométricas inversas.
- Ejemplos.
- Definición razonada de las razones trigonométricas de un ángulo agudo.
Videotutorial
Videotutorial
Videotutorial
- Si pulsas el botón "EJERCICIO" cambiarán los datos del triángulo.
- Si pulsas el botón "ángulo" cambiará el ángulo al que se le calculan las razones trigonométricas.
- Si pulsas el botón "OTRAS RAZONES" alternararás entre las razones trigonométricas y sus recíprocas.
- Si pulsas el botón "AUTOEVALUACIÓN" podrás realizar una tanda de ejercicios para comprobar lo que sabes.
Relaciones fundamentales de la trigonometría
Relaciones fundamentales de la trigonometría
1. 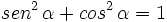
2. 
3. 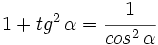
Demostración:
1. 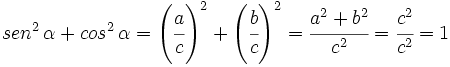
ya que, por el teorema de Pitágoras, 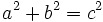 .
.
2. 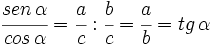
3. 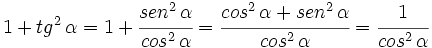
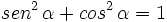
Videotutorial
Videotutorial
Ejercicio resuelto: Razones trigonométricas de un ángulo agudo
1. Conociendo  , calcular
, calcular 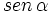 y
y 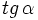 .
.
2. Conociendo 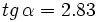 , calcular
, calcular 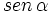 y
y 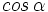 .
.
Solución:
Hay que usar las relaciones fundamentales de la trigonometría para despejar la razón trigonométrica desconocida:
1. 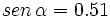 y
y 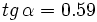
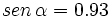 y
y 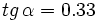
Razones trigonométricas de algunos ángulos importantes
A continuación las razones trigonométricas de algunos ángulos que es conveniente recordar:
| Grados | sen | cos | tg | cosec | sec | cot |
|---|---|---|---|---|---|---|
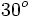
| 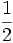
| 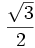
| 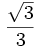
| 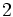
| 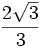
| 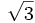
|
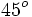
| 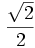
| 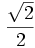
| 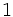
| 
| 
| 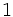
|
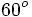
| 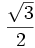
| 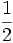
| 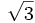
| 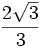
| 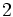
| 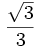
|
- Dos ángulos agudos se dicen complementarios si suman 90º.
- El seno de un ángulo agudo coincide con el coseno de su complementario.
- La tangente de un ángulo agudo coincide con la cotangente de su complementario.
- La secante de un ángulo agudo coincide con la cesecante de su complementario.
- Apoyándonos en un triángulo equilátero de lado unidad, en este vídeo determinamos las razones trigonométricas de los ángulos de 30º y 60º.
- También determinamos las razones trigonométricas del ángulo de 45º; para ello nos servimos de un triángulo rectángulo de catetos unitarios.
- Las razones trigonométricas en cuestión deben memorizarse.