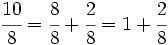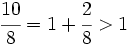El significado de las fracciones (1º ESO)
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 16:37 23 sep 2016 Coordinador (Discusión | contribuciones) (→Fraciones propias e impropias) ← Ir a diferencia anterior |
Revisión de 16:47 23 sep 2016 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 12: | Línea 12: | ||
| {{p}} | {{p}} | ||
| {{Tabla50|celda2=[[Imagen:fraccion.gif|center|400px]]|celda1= | {{Tabla50|celda2=[[Imagen:fraccion.gif|center|400px]]|celda1= | ||
| - | {{Caja_Amarilla|texto=Una '''fracción''' es un número que expresa una cantidad determinada de porciones que se toman de un todo dividido en partes iguales. | + | {{Caja_Amarilla|texto= |
| + | *Una '''fracción''' es un número que expresa una cantidad determinada de porciones que se toman de un todo dividido en partes iguales. | ||
| Se representa <math>\frac{a}{b}\;</math>, o bien, <math>a/b\;</math>: | Se representa <math>\frac{a}{b}\;</math>, o bien, <math>a/b\;</math>: | ||
| - | *A <math>b\;</math> se le llama '''denominador''' y representa las partes en que se divide la unidad. | + | :*A {{sube|porcentaje=15%|contenido=<math>b\;</math>}} se le llama '''denominador''' y representa las partes en que se divide la unidad. |
| - | *A <math>a\;</math> se le llama '''numerador''' y representa las porciones que tomamos. | + | :*A {{sube|porcentaje=15%|contenido=<math>a\;</math>}} se le llama '''numerador''' y representa las porciones que tomamos. |
| + | |||
| + | *El '''valor''' de la fracción es el número que resulta de dividir el numerador entre el denominador. | ||
| }} | }} | ||
| + | }} | ||
| + | |||
| + | {{p}} | ||
| + | {{Ejemplo_simple|titulo=Ejemplo:|contenido= | ||
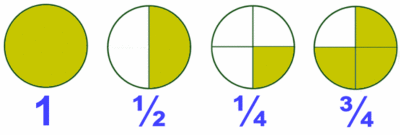
| + | En el dibujo de la derecha tienes algunas fracciones cuyo valor se obtiene dividiendo el numerador entre el denominador: | ||
| + | |||
| + | <math>\cfrac{1}{1}= 1 \, ; \qquad \cfrac{1}{2}= 0.5 \, ; \qquad \cfrac{1}{4}=0.25 \, ; \qquad \cfrac{3}{4}= 0.75</math> | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| Línea 45: | Línea 55: | ||
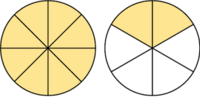
| {{Teorema_sin_demo|titulo=Proposición|enunciado=Toda fracción impropia se puede expresar como un número entero más una fracción propia, es decir, como '''número mixto'''. | {{Teorema_sin_demo|titulo=Proposición|enunciado=Toda fracción impropia se puede expresar como un número entero más una fracción propia, es decir, como '''número mixto'''. | ||
| }} | }} | ||
| + | {{p}} | ||
| {{Ejemplo_simple|titulo=Ejemplo:|contenido= | {{Ejemplo_simple|titulo=Ejemplo:|contenido= | ||
| <math>\cfrac{10}{8}= \cfrac{8}{8} + \cfrac{2}{8} = 1 +\cfrac{2}{8}</math> | <math>\cfrac{10}{8}= \cfrac{8}{8} + \cfrac{2}{8} = 1 +\cfrac{2}{8}</math> | ||
Revisión de 16:47 23 sep 2016
Menú:
| Enlaces internos | Para repasar | Para ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadora |
Tabla de contenidos |
(Pág. 122)
El significado de las fracciones
Cuando necesitamos expresar cantidades con partes de la unidad, además de los números decimales, disponemos de las fracciones.
Se representa
|
En el dibujo de la derecha tienes algunas fracciones cuyo valor se obtiene dividiendo el numerador entre el denominador:
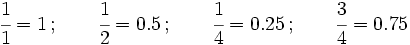
Fracciones propias e impropias
Proposición Toda fracción impropia se puede expresar como un número entero más una fracción propia, es decir, como número mixto. |
Ejercicios propuestos
|
Ejercicios propuestos: El significado de las fracciones |
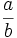 , o bien,
, o bien, 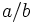 :
: