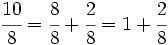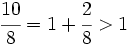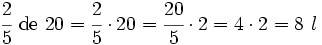El significado de las fracciones (1º ESO)
De Wikipedia
| Revisión de 07:54 24 sep 2016 Coordinador (Discusión | contribuciones) (→La fracción como operador) ← Ir a diferencia anterior |
Revisión de 07:57 24 sep 2016 Coordinador (Discusión | contribuciones) (→La fracción como operador) Ir a siguiente diferencia → |
||
| Línea 109: | Línea 109: | ||
| |enunciado= | |enunciado= | ||
| Si de un depósito de agua, en el que caben 20 l, sólo están llenas las 2/5 partes, ¿cuánta agua hay en el depósito? | Si de un depósito de agua, en el que caben 20 l, sólo están llenas las 2/5 partes, ¿cuánta agua hay en el depósito? | ||
| - | |sol= | + | |sol={{Tabla75|celda2= |
| - | [[Imagen:deposito.png|200px|right]]Se divide la capacidad total del depósito entre 5, que es el número de partes en que hemos dividido la unidad (el depósito). El resultado se multiplica por 2, que son las partes de depósito que estan llenas: | + | [[Imagen:deposito.png|250px|right]]|celda1=Se divide la capacidad total del depósito entre 5, que es el número de partes en que hemos dividido la unidad (el depósito). El resultado se multiplica por 2, que son las partes de depósito que estan llenas: |
| :<math>\cfrac{2}{5} \ \mbox{de} \ 20=\cfrac{2}{5} \cdot 20 = \cfrac{20}{5} \cdot 2= 4 \cdot 2 = 8 \ l</math> | :<math>\cfrac{2}{5} \ \mbox{de} \ 20=\cfrac{2}{5} \cdot 20 = \cfrac{20}{5} \cdot 2= 4 \cdot 2 = 8 \ l</math> | ||
| + | }} | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
Revisión de 07:57 24 sep 2016
| Enlaces internos | Para repasar | Para ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadora |
Tabla de contenidos |
(Pág. 122)
Las fracciones
Cuando necesitamos expresar cantidades con partes de la unidad, además de los números decimales, disponemos de las fracciones.
|
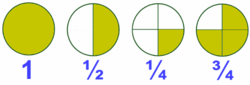
En la Fig. 1 tienes algunos ejemlos de fracciones representadas mendiante los llamados diagramas de tarta.
El valor de cada fracción se obtiene dividiendo el numerador entre el denominador:
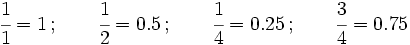
Fíjate que la unidad se puede representar mediante una fracción que tenga el mismo numerador que denominador.
Fracciones propias e impropias
Proposición Toda fracción impropia se puede expresar como un número entero más una fracción propia, es decir, como número mixto. |
|
Actividad: Números racionales
Solución: Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones:
|
La fracción como operador
Procedimiento
Para calcular la fracción de una cantidad, se divide la cantidad entre el denominador y se multiplica por el numerador.
Ejercicio resuelto: La fracción como operador
Si de un depósito de agua, en el que caben 20 l, sólo están llenas las 2/5 partes, ¿cuánta agua hay en el depósito?
Ejercicios propuestos
|
Ejercicios propuestos: El significado de las fracciones |
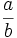 , o bien,
, o bien, 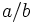 :
:


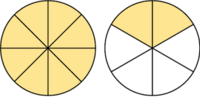
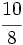 es impropia. Es mayor que la unidad y podemos expresarla como número mixto (Ver Fig. 2):
es impropia. Es mayor que la unidad y podemos expresarla como número mixto (Ver Fig. 2):