Problemas de proporcionalidad inversa (1º ESO)
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 11:37 27 sep 2016 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 12:57 28 sep 2016 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 9: | Línea 9: | ||
| (Pág. 156) | (Pág. 156) | ||
| ==Método de reducción a la unidad== | ==Método de reducción a la unidad== | ||
| + | {{Teorema_sin_demo|titulo=Procedimiento|enunciado=El '''método de reducción a la unidad''' consiste en averiguar el valor la segunda magnitud si la primera vale 1 (la unidad). A partir de esa información, es fácil sacar los demás valores de la segunda magnitud a partir de los de la primera, ya que sólo tendremos que dividir la primera magnitud por dicho valor.}} | ||
| + | {{p}} | ||
| + | {{Ejemplo_simple|titulo=Ejemplo:|contenido= | ||
| + | Dos grifos tardan en llenar una piscina en 6 horas. ¿Cuánto tiempo taradarán 3 grifos? | ||
| + | ---- | ||
| + | '''Solución:''' | ||
| + | |||
| + | Primero averiguamos lo que tarda 1 grifo (la unidad): | ||
| + | |||
| + | Nº grifos Tiempo (h) | ||
| + | ---------- ---------- | ||
| + | 2 --------> 6 | ||
| + | 1 --------> x | ||
| + | |||
| + | :<math>x=6 \dcot 2 = 12</math> h | ||
| + | |||
| + | A partir del tiempo que tarda 1 grifo es fácil sacar el que tardan 3 grifos: | ||
| + | |||
| + | Nº grifos Tiempo (h) | ||
| + | ---------- ---------- | ||
| + | 1 --------> 12 | ||
| + | 3 --------> x | ||
| + | |||
| + | :<math>x = \cfrac {12}{3} = 4 </math> h | ||
| + | }} | ||
| + | {{p}} | ||
| ==Regla de tres inversa== | ==Regla de tres inversa== | ||
| {{p}} | {{p}} | ||
Revisión de 12:57 28 sep 2016
Menú:
| Enlaces internos | Para repasar | Para ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadora |
Tabla de contenidos |
(Pág. 156)
Método de reducción a la unidad
Procedimiento
El método de reducción a la unidad consiste en averiguar el valor la segunda magnitud si la primera vale 1 (la unidad). A partir de esa información, es fácil sacar los demás valores de la segunda magnitud a partir de los de la primera, ya que sólo tendremos que dividir la primera magnitud por dicho valor.
Dos grifos tardan en llenar una piscina en 6 horas. ¿Cuánto tiempo taradarán 3 grifos?
Solución:
Primero averiguamos lo que tarda 1 grifo (la unidad):
Nº grifos Tiempo (h)
---------- ----------
2 --------> 6
1 --------> x
- No se pudo entender (función desconocida\dcot): x=6 \dcot 2 = 12
h
A partir del tiempo que tarda 1 grifo es fácil sacar el que tardan 3 grifos:
Nº grifos Tiempo (h)
---------- ----------
1 --------> 12
3 --------> x
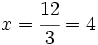h
Regla de tres inversa
Actividades
Actividades: Problemas de proporcionalidad inversa Descripción: Ejercicios propuestos
 Ejercicios propuestos: Problemas de proporcionalidad inversa (Pág. 157)
|
