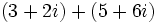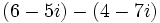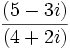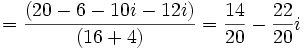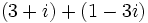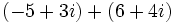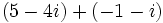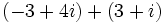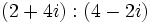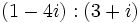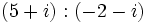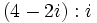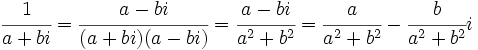Números complejos: Operaciones (1ºBach)

De Wikipedia

(Diferencia entre revisiones)
Revisión de 18:45 30 sep 2014
Coordinador (Discusión | contribuciones)
(→Operaciones con números complejos en forma binómica)
← Ir a diferencia anterior		 Revisión de 11:59 2 oct 2016
Coordinador (Discusión | contribuciones)
(→Operaciones con números complejos en forma binómica)
Ir a siguiente diferencia →
Línea 9: Línea 9:
{{Caja_Amarilla|texto= {{Caja_Amarilla|texto=
* '''Suma:''' <math>\,(a + bi) + (c + di) = (a + c) + (b + d)i</math> * '''Suma:''' <math>\,(a + bi) + (c + di) = (a + c) + (b + d)i</math>
 +
* '''Resta:''' <math>\,(a + bi) - (c + di) = (a - c) + (b - d)i</math> * '''Resta:''' <math>\,(a + bi) - (c + di) = (a - c) + (b - d)i</math>
 +
* '''Multiplicación:''' <math>\,(a + bi) (c + di) = ac + bci + adi + bd i^2 = (ac - bd) + (bc + ad)i</math> * '''Multiplicación:''' <math>\,(a + bi) (c + di) = ac + bci + adi + bd i^2 = (ac - bd) + (bc + ad)i</math>
 +
* '''División:''' <math>\,\frac{(a + bi)}{(c + di)} = \frac{(a + bi) (c - di)}{(c + di) (c - di)} = \left({ac + bd \over c^2 + d^2}\right) + \left( {bc - ad \over c^2 + d^2} \right)i\, </math>, siempre que <math>c+di\,</math> no sea nulo. * '''División:''' <math>\,\frac{(a + bi)}{(c + di)} = \frac{(a + bi) (c - di)}{(c + di) (c - di)} = \left({ac + bd \over c^2 + d^2}\right) + \left( {bc - ad \over c^2 + d^2} \right)i\, </math>, siempre que <math>c+di\,</math> no sea nulo.
}} }}
Línea 44: Línea 47:
{{ejemplo {{ejemplo
|titulo=Ejemplos: ''Operaciones con complejos en forma binómica'' |titulo=Ejemplos: ''Operaciones con complejos en forma binómica''
-|enunciado=:Efectúa las siguientes operaciones:+|enunciado=Efectúa las siguientes operaciones:
-:# <math>\,(3 + 2i) + (5 + 6i)</math>+# <math>\,(3 + 2i) + (5 + 6i)</math>
-:# <math>\,(6 - 5i) - (4 - 7i)</math>+# <math>\,(6 - 5i) - (4 - 7i)</math>
-:# <math>\,(3 + 4i) (2 - 5i)</math>+# <math>\,(3 + 4i) (2 - 5i)</math>
-:# <math>\,\frac{(5 - 3i)}{(4 + 2i)}</math>+# <math>\,\frac{(5 - 3i)}{(4 + 2i)}</math>
|sol= |sol=
-# <math>\,(3 + 2i) + (5 + 6i)=3 + 5 + 2i + 6i=8 + 8i</math>+1. <math>\,(3 + 2i) + (5 + 6i)=3 + 5 + 2i + 6i=8 + 8i</math>
-# <math>\,(6 - 5i) - (4 - 7i)=6-4-5i+7i=2+2i</math>+ 
-# <math>\,(3 + 4i) (2 - 5i)=6-15i+8i-20i^2=6-7i+20=26-7i</math>+2. <math>\,(6 - 5i) - (4 - 7i)=6-4-5i+7i=2+2i</math>
-# <math>\,\frac{(5 - 3i)}{(4 + 2i)}=\frac{(5 - 3i)(4-2i)}{(4 + 2i)(4-2i)}=\frac{(20-10i-12i+6i^2)}{(16-8i+8i-4i^2)}=\frac{(20-6-10i-12i)}{(16+4)}=\frac{14}{20}-\frac{22}{20}i</math>+ 
 +3. <math>\,(3 + 4i) (2 - 5i)=6-15i+8i-20i^2=6-7i+20=26-7i</math>
 + 
 +4. <math>\,\frac{(5 - 3i)}{(4 + 2i)}=\frac{(5 - 3i)(4-2i)}{(4 + 2i)(4-2i)}=\frac{(20-10i-12i+6i^2)}{(16-8i+8i-4i^2)}=</math>
 + 
 +::::<math>=\frac{(20-6-10i-12i)}{(16+4)}=\frac{14}{20}-\frac{22}{20}i</math>
}} }}
{{p}} {{p}}
-{{ejercicio 
-|titulo=Ejercicios: ''Operaciones con números complejos en forma binómica'' 
-|cuerpo= 
{{Video_enlace {{Video_enlace
|titulo1= 2 ejercicios (Suma) |titulo1= 2 ejercicios (Suma)
Línea 106: Línea 111:
|url1=http://matematicasbachiller.com/videos/1-bachillerato/matematicas-de-primero-de-bachillerato/12-numeros-complejos/1001-dos-ejercicios-9#.VCr5_ha7ZV8 |url1=http://matematicasbachiller.com/videos/1-bachillerato/matematicas-de-primero-de-bachillerato/12-numeros-complejos/1001-dos-ejercicios-9#.VCr5_ha7ZV8
|sinopsis=Videotutorial. |sinopsis=Videotutorial.
-}} 
}} }}
{{p}} {{p}}

Revisión de 11:59 2 oct 2016

Menú:
Enlaces internos Para repasar o ampliar Enlaces externos
Indice
Descartes
Manual Casio
 WIRIS
Geogebra
Calculadoras

Operaciones con números complejos en forma binómica

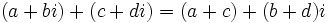
  • Suma: \,(a + bi) + (c + di) = (a + c) + (b + d)i
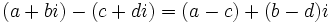
  • Resta: \,(a + bi) - (c + di) = (a - c) + (b - d)i
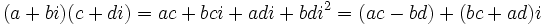
  • Multiplicación: \,(a + bi) (c + di) = ac + bci + adi + bd i^2 = (ac - bd) + (bc + ad)i
  • División: 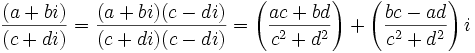\,\frac{(a + bi)}{(c + di)} = \frac{(a + bi) (c - di)}{(c + di) (c - di)} = \left({ac + bd \over c^2 + d^2}\right) + \left( {bc - ad \over c^2 + d^2} \right)i\,, siempre que 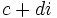c+di\, no sea nulo.

Suma de números complejos (8´53")     Sinopsis:

Videotutorial.

Producto de números complejos (11´26")     Sinopsis:

Videotutorial.

Cociente de números complejos (7´45")     Sinopsis:

Videotutorial.

Potenciación de números complejos expresados en forma binómica (3´50")     Sinopsis:

Las potencias de números complejos hacen uso de la fórmula del binomio de Newton. No obstante, son mucho más fáciles si se realizan en forma polar como se verá en otro apartado de este tema.

ejercicio

Ejemplos: Operaciones con complejos en forma binómica

Efectúa las siguientes operaciones:

  1. \,(3 + 2i) + (5 + 6i)
  2. \,(6 - 5i) - (4 - 7i)
  3. \,(3 + 4i) (2 - 5i)
  4. \,\frac{(5 - 3i)}{(4 + 2i)}
Solución:

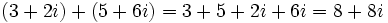
1. \,(3 + 2i) + (5 + 6i)=3 + 5 + 2i + 6i=8 + 8i

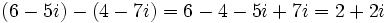
2. \,(6 - 5i) - (4 - 7i)=6-4-5i+7i=2+2i

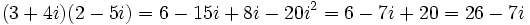
3. \,(3 + 4i) (2 - 5i)=6-15i+8i-20i^2=6-7i+20=26-7i

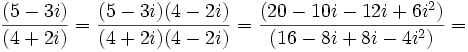
4. \,\frac{(5 - 3i)}{(4 + 2i)}=\frac{(5 - 3i)(4-2i)}{(4 + 2i)(4-2i)}=\frac{(20-10i-12i+6i^2)}{(16-8i+8i-4i^2)}=

=\frac{(20-6-10i-12i)}{(16+4)}=\frac{14}{20}-\frac{22}{20}i

2 ejercicios (Suma) (5´55")     Sinopsis:

Videotutorial.

3 ejercicios (Ecuaciones con soluciones complejas) (9´24")     Sinopsis:

Videotutorial.

3 ejercicios (Producto) (9´19")     Sinopsis:

Videotutorial.

3 ejercicios (Producto) (7´05")     Sinopsis:

Videotutorial.

2 ejercicios (Cociente) (6´46")     Sinopsis:

Videotutorial.

3 ejercicios (Cociente) (8´11")     Sinopsis:

Videotutorial.

3 ejercicios (Cociente) (7´19")     Sinopsis:

Videotutorial.

2 ejercicios (Potencia) (6´49")     Sinopsis:

Videotutorial.

ejercicio

Actividad interactiva: Operaciones con números complejos

Suma: Efectúa las siguientes sumas de números complejos en tu cuaderno y haz una comprobación posterior en la escena:
  1. \,(3 + i) + (1 - 3i)
  2. \,(-5 + 3i) + (6 + 4i)
  3. \,(5 - 4i) + (-1 - i)
  4. \,(-3 + 4i)+(3 + i)

Actividad:
Utiliza el deslizador verde para comprobar cómo se obtiene la suma de dos complejos por el "método del paralelogramo"

Mueve los puntos azules para modificar los datos.


Click aquí si no se ve bien la escena
Resta: Efectúa las siguientes restas de números complejos en tu cuaderno y haz una comprobación posterior en la escena:
  1. \,(-5 + 3i) - (4 + 2i)
  2. \,(5 -2i) -(1+ 4i)
  3. \,(5 - 4i) - (-1 - i)
  4. \,(-3 + 4i)-(3 - 2i)

Actividad:
Utiliza el deslizador verde para comprobar cómo se obtiene la resta de dos complejos por el "método del paralelogramo"

Mueve los puntos azules para modificar los datos.


Click aquí si no se ve bien la escena


Otro modo de restar números complejos es sumar el opuesto: puedes comprobarlo en la siguiente figura:

Click aquí si no se ve bien la escena
Producto: Efectúa las siguientes multiplicaciones en tu cuaderno y haz una comprobación posterior en la escena:
  1. \,(-2 -2i) (1 + 3i)
  2. \,(2 + 3i)(5-6i)
  3. \,(2+3i)(-2-3i)
  4. \,(-1-2i)(-1+2i)

Actividad:
Utiliza el deslizador verde para comprobar cómo se obtiene el producto de dos complejos, a partir del triángulo construido a partir del primer número complejo, el origen de coordenadas y el punto (1,0).

Mueve los puntos azules para modificar los datos.


Click aquí si no se ve bien la escena
División: Efectúa las siguientes divisiones en tu cuaderno y compruébalas en la escena:
  1. \,(2+4i):(4-2i)
  2. \,(1-4i):(3+i)
  3. \,(5+i):(-2-i)
  4. \,(4-2i):i

Actividad:
Utiliza el deslizador verde para comprobar cómo se obtiene el cociente de dos complejos, a partir del triángulo construido a partir de los dos.

Mueve los puntos azules para modificar los datos.


Click aquí si no se ve bien la escena

Propiedades de las operaciones con números complejos

  • El 0 es el elemento neutro de la suma.
  • Todo número complejo, a+bi\,, tiene un opuesto, -a-bi\,
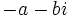
  • El 1 es el elemento neutro del producto.
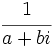  • Todo número complejo, a+bi\,, distinto de 0, tiene inverso, \cfrac{1}{a+bi}:
\cfrac{1}{a+bi}=\cfrac{a-bi}{(a+bi)(a-bi)}=\cfrac{a-bi}{a^2+b^2}=\cfrac{a}{a^2+b^2}-\cfrac{b}{a^2+b^2}i
Obtenido de "http://maralboran.org/wikipedia/index.php/N%C3%BAmeros_complejos:_Operaciones_%281%C2%BABach%29"
Herramientas personales
* AVISO: Para que te funcionen los applets de Java debes usar Internet Explorer y seguir las instrucciones de la Ayuda del menu de la izquierda