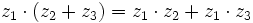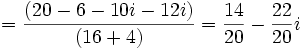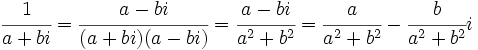Números complejos: Operaciones (1ºBach)
De Wikipedia
| Revisión de 13:20 4 oct 2016 Coordinador (Discusión | contribuciones) (→Propiedades de las operaciones con números complejos) ← Ir a diferencia anterior |
Revisión de 13:27 4 oct 2016 Coordinador (Discusión | contribuciones) (→Propiedades de las operaciones con números complejos) Ir a siguiente diferencia → |
||
| Línea 169: | Línea 169: | ||
| {{Teorema_sin_demo|titulo=Propiedades|enunciado= | {{Teorema_sin_demo|titulo=Propiedades|enunciado= | ||
| *'''Propiedades de la suma:''' | *'''Propiedades de la suma:''' | ||
| - | **'''Asociativa'''. | + | **'''Asociativa''': <math>z_1+(z_2+z_3)=(z_1+z_2)+z_1\;</math> |
| - | **'''Conmutativa'''. | + | **'''Conmutativa''': <math>z_1+z_2=z_2+z_1\;</math> |
| **Existencia de '''elemento neutro''': El 0 es el elemento neutro de la suma. | **Existencia de '''elemento neutro''': El 0 es el elemento neutro de la suma. | ||
| **Existencia de '''opuesto''': Todo número complejo, <math>a+bi\,</math>, tiene un opuesto, <math>-a-bi\,</math> | **Existencia de '''opuesto''': Todo número complejo, <math>a+bi\,</math>, tiene un opuesto, <math>-a-bi\,</math> | ||
| *'''Propiedades del producto:''' | *'''Propiedades del producto:''' | ||
| - | **'''Asociativa'''. | + | **'''Asociativa''': <math>z_1 \cdot (z_2 \cdot z_3)=(z_1 \cdot z_2) \cdot z_1</math> |
| - | **'''Conmutativa'''. | + | **'''Conmutativa''': <math>z_1 \cdot z_2=z_2 \cdot z_1</math> |
| **Existencia de '''elemento neutro''': El 1 es el elemento neutro del producto. | **Existencia de '''elemento neutro''': El 1 es el elemento neutro del producto. | ||
| **Existencia de '''inverso''': Todo número complejo, <math>a+bi\,</math>, distinto de 0, tiene inverso, <math>\cfrac{1}{a+bi}</math>: | **Existencia de '''inverso''': Todo número complejo, <math>a+bi\,</math>, distinto de 0, tiene inverso, <math>\cfrac{1}{a+bi}</math>: | ||
| ::<math>\cfrac{1}{a+bi}=\cfrac{a-bi}{(a+bi)(a-bi)}=\cfrac{a-bi}{a^2+b^2}=\cfrac{a}{a^2+b^2}-\cfrac{b}{a^2+b^2}i</math> | ::<math>\cfrac{1}{a+bi}=\cfrac{a-bi}{(a+bi)(a-bi)}=\cfrac{a-bi}{a^2+b^2}=\cfrac{a}{a^2+b^2}-\cfrac{b}{a^2+b^2}i</math> | ||
| + | |||
| + | *'''Propiedad distributiva del producto respecto de la suma:''' <math>z_1\cdot(z_2+z_3)=z_1 \cdot z_2 + z_1 \cdot z_3</math> | ||
| }} | }} | ||
| [[Categoría: Matemáticas]][[Categoría: Geometría]][[Categoría: Números]] | [[Categoría: Matemáticas]][[Categoría: Geometría]][[Categoría: Números]] | ||
Revisión de 13:27 4 oct 2016
| Enlaces internos | Para repasar o ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadoras |
Operaciones con números complejos en forma binómica
- Suma:
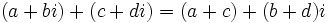
- Resta:
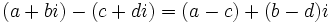
- Multiplicación:
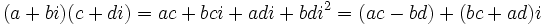
- División:
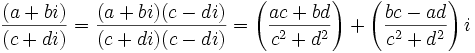 , siempre que
, siempre que 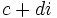 no sea nulo.
no sea nulo.
- Definición de suma de números complejos en forma binómica.
- Representación gráfica.
- Ejemplos.
- Propiedades.
- Definición de producto de números complejos en forma binómica.
- Ejemplos.
- Propiedades.
- Definición de cociente de números complejos en forma binómica.
- Ejemplos.
Las potencias de números complejos hacen uso de la fórmula del binomio de Newton. No obstante, son mucho más fáciles si se realizan en forma polar como se verá en otro apartado de este tema.
Ejemplos: Operaciones con complejos en forma binómica
Efectúa las siguientes operaciones:
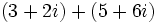
Solución:
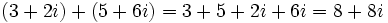
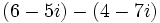
Solución:
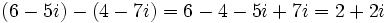

Solución:
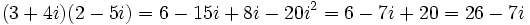
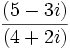
Solución:
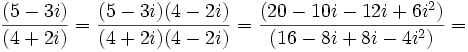
Videotutorial.
Videotutorial.
Videotutorial.
Videotutorial.
Videotutorial.
Videotutorial.
Videotutorial.
Videotutorial.
Representación gráfica de las operaciones con complejos en forma binómica
En esta escena podrás ver como se representa la suma de números complejos en forma binómica.
En esta escena podrás ver como se representa la resta de números complejos en forma binómica.
En esta escena podrás ver como se representa la multiplicación de números complejos en forma binómica.
En esta escena podrás ver como se representa la división de números complejos en forma binómica.
Propiedades de las operaciones con números complejos
Propiedades
- Propiedades de la suma:
- Asociativa:
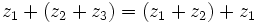
- Conmutativa:
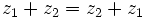
- Existencia de elemento neutro: El 0 es el elemento neutro de la suma.
- Existencia de opuesto: Todo número complejo,
 , tiene un opuesto,
, tiene un opuesto, 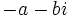
- Asociativa:
- Propiedades del producto:
- Asociativa:
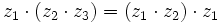
- Conmutativa:
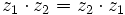
- Existencia de elemento neutro: El 1 es el elemento neutro del producto.
- Existencia de inverso: Todo número complejo,
 , distinto de 0, tiene inverso,
, distinto de 0, tiene inverso, 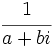 :
:
- Asociativa:
- Propiedad distributiva del producto respecto de la suma: