Números complejos: Operaciones en forma polar (1ºBach)
De Wikipedia
| Revisión de 14:55 5 oct 2016 Coordinador (Discusión | contribuciones) (→Potencias de números complejos en forma polar) ← Ir a diferencia anterior |
Revisión de 14:56 5 oct 2016 Coordinador (Discusión | contribuciones) (→División de números complejos en forma polar) Ir a siguiente diferencia → |
||
| Línea 119: | Línea 119: | ||
| {{Ejemplo_simple|titulo=Ejemplo:|contenido=:<math>6_{60^\circ} : 3_{45^\circ}=\Big( \cfrac{6}{3} \, \Big)_{60^\circ - 45^\circ}=2_{15^\circ}</math>}} | {{Ejemplo_simple|titulo=Ejemplo:|contenido=:<math>6_{60^\circ} : 3_{45^\circ}=\Big( \cfrac{6}{3} \, \Big)_{60^\circ - 45^\circ}=2_{15^\circ}</math>}} | ||
| {{p}} | {{p}} | ||
| - | {{AI2|titulo=Actividad interactiva: ''División de complejos en forma polar''|cuerpo= | + | |
| - | {{ai_cuerpo | + | {{AI_enlace |
| - | |enunciado=:Efectúa las siguientes divisiones de complejos en forma polar y compruébalo en la escena: | + | |titulo1=Actividad: ''División de complejos en forma polar'' |
| + | |descripcion=Efectúa las siguientes divisiones de complejos en forma polar y compruébalo en la escena: | ||
| ::'''a)''' <math>5_{150^\circ} : 2_{30^\circ}</math> | ::'''a)''' <math>5_{150^\circ} : 2_{30^\circ}</math> | ||
| ::'''b)''' <math>6_{225^\circ} : 3_{75^\circ}</math> | ::'''b)''' <math>6_{225^\circ} : 3_{75^\circ}</math> | ||
| {{p}} | {{p}} | ||
| - | |actividad=Mueve el punto azul o, con el botón derecho sobre él, elige "Redefine" del menú contextual, para modificar el valor del número complejo. | + | Mueve el punto azul o, con el botón derecho sobre él, elige "Redefine" del menú contextual, para modificar el valor del número complejo. |
| Modifica el exponente con el deslizador verde. | Modifica el exponente con el deslizador verde. | ||
| Línea 137: | Línea 138: | ||
| name=myframe | name=myframe | ||
| </iframe></center> | </iframe></center> | ||
| - | <center>[http://maralboran.org/web_ma/geogebra/figuras/complejos_div_polar.html '''Click''' aquí si no se ve bien la escena]</center> | + | |url1=http://maralboran.org/web_ma/geogebra/figuras/complejos_div_polar.html |
| - | + | ||
| - | + | ||
| - | Utiliza el deslizador verde para comprobar cómo se obtiene el cociente de dos complejos, a partir del triángulo construido a partir de los dos.. | + | |
| - | }} | + | |
| }} | }} | ||
| {{p}} | {{p}} | ||
Revisión de 14:56 5 oct 2016
| Enlaces internos | Para repasar o ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadoras |
Tabla de contenidos |
Multiplicación de números complejos en forma polar
Producto de complejos en forma polar
El producto de dos numeros complejos en forma polar es otro complejo en forma polar cuyo módulo es el producto de los módulos y el argumento la suma de los argumentos de los respectivos complejos.
|
|
Expresando los complejos en forma trigonométrica:
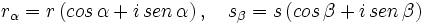
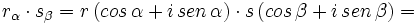
Videotutorial.
Efectúa las siguientes multiplicaciones de complejos en forma polar y compruébalo en la escena:
- a)

- b)
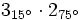
- a)
Mueve los puntos azules o, con el botón derecho sobre ellos, elige "Redefine" del menú contextual, para modificar los valores de los números complejos.
Potencias de números complejos en forma polar
Potencia de un complejo en forma polar
- La potencia n-ésima de un compejo se obtiene de la siguiente manera:
|
|
La potencia n-ésima de un compejo es el resultado de multiplicar dicho complejo por sí mismo n veces, por tanto, aplicando la fórmula del producto:
Videotutorial.
Videotutorial.
Videotutorial.
Efectúa las siguientes potencias de complejos en forma polar y compruébalo en la escena:
- a)
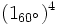 b)
b)  c)
c)  d)
d) 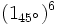
- a)
Mueve los puntos azules o, con el botón derecho sobre ellos, elige "Redefine" del menú contextual, para modificar los valores de los números complejos.
Fórmula de Moivre
Fórmula de Moivre
Basta aplicar la fórmula de la potencia de un complejo en forma polar y tener en cuenta la forma trigonométrica de un número complejo:
División de números complejos en forma polar
División de complejos en forma polar
La división de dos numeros complejos en forma polar es otro complejo en forma polar cuyo módulo es el cociente de los módulos y el argumento la diferencia de los argumentos de los respectivos complejos.
|
|
Videotutorial.
Efectúa las siguientes divisiones de complejos en forma polar y compruébalo en la escena:
- a)

- b)
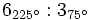
- a)
Mueve el punto azul o, con el botón derecho sobre él, elige "Redefine" del menú contextual, para modificar el valor del número complejo.
Modifica el exponente con el deslizador verde.
Radicación de números complejos en forma polar
Un número complejo 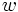 es una raíz n-ésima de otro complejo
es una raíz n-ésima de otro complejo 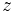 si se cumple que
si se cumple que 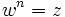 .
.
Raíces de un complejo
- Un número complejo
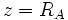 tiene exactamente n raíces n-ésimas
tiene exactamente n raíces n-ésimas 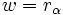 , que se obtienen de la siguiente manera:
, que se obtienen de la siguiente manera:
![r_\alpha : \begin{cases} r=\sqrt[n]{R} \\ \alpha=\cfrac{A+2k \pi}{n}\, , \quad k=0,1,\cdots,(n-1) \end{cases}](/wikipedia/images/math/4/a/5/4a5dd4f3f68e14f0c8013ccc27085e5e.png)
Por la definición de raíz n-ésima:
Igualando módulos ya rgumentos:
Ejemplo: Raíces de un complejo
- Calcula:
![\sqrt[3]{1+i}](/wikipedia/images/math/8/8/3/883e0a5f87d5879d879d48e3bbe5789d.png) :
:
Primero pasamos el complejo 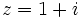 a forma polar:
a forma polar:
Así, 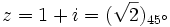
Ahora procedemos a calcular sus 3 raíces cubicas:
![\sqrt[3]{(\sqrt{2})_{45^\circ}}=r_\alpha](/wikipedia/images/math/c/5/e/c5e849c7713f59a373e993c0d21a8bd5.png) , siendo
, siendo ![\begin{cases} r=\sqrt[3]{\sqrt{2}} \\ \alpha=\cfrac{45^\circ +2k \pi}{3}\, , \quad k=0,1,2 \end{cases}](/wikipedia/images/math/e/3/3/e338be4b3b0010eb3dd1abb6ea6669f0.png)
De donde ![r_\alpha : \begin{cases} r=\sqrt[6]{2} \\ \alpha= 15^\circ \, , \quad 135^\circ \, , \quad 257^\circ \end{cases}](/wikipedia/images/math/d/9/7/d978739b21c71e554a372161eb06a8b7.png)
Soluciones:
Videotutorial.
|
Ejercicios:Radicación de números complejos expresados en forma polar Videotutorial. Videotutorial. Videotutorial. |
|
Actividad interactiva: Raíces de complejos en forma polar
Actividad: Mueve el punto azul o, con el botón derecho sobre él, elige "Redefine" del menú contextual, para modificar el valor del número complejo. Modifica el índice de la raíz con el deslizador verde. |
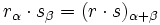
![=r \cdot s \, [cos \alpha \, \cos \beta + i \, cos \alpha \, sen \beta + i \, sen \, \alpha \, cos \, \beta + i^2 \, sen \, \alpha \, sen \, \beta ]=](/wikipedia/images/math/5/9/1/591804e8ee81496a02138c096a8d2d59.png)
![=r \cdot s \, [cos \alpha \, \cos \beta - sen \, \alpha \, sen \, \beta+ i \, ( cos \alpha \, sen \beta + sen \, \alpha \, cos \, \beta )]=](/wikipedia/images/math/2/f/c/2fcccb290acf0ed109301fe82ce33846.png)
![=r \cdot s \, [cos (\alpha + \beta ) + i \, sen \, ( \alpha + \beta )]=(r \cdot s)_{\alpha + \beta}](/wikipedia/images/math/7/6/d/76d54879d578a64886a5aeeafb79b32e.png)
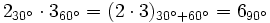
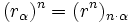
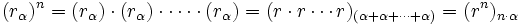
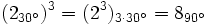
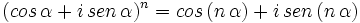
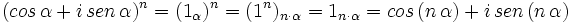
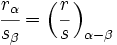
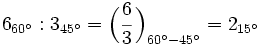
![\sqrt[n]{z}=w \iff z=w^n \iff (R_A)=(r_\alpha)^n \iff R_A=(r^n)_{n \, \alpha}](/wikipedia/images/math/b/7/7/b7781ba8724c717e4f2b2423267ad5bf.png)
![R_A=(r^n)_{n \, \alpha} \iff \begin{cases} r^n=R \iff r=\sqrt[n]{R} \\ n \, \alpha = A + 2k \pi \iff \alpha=\cfrac{A+2k \pi}{n}\, , \quad k=0,1,\cdots,(n-1) \end{cases}](/wikipedia/images/math/c/8/0/c808af8500c52fdd7279ea16c43c86cc.png)
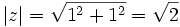
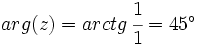
![(\sqrt[6]{2})_{15^\circ} \, , \quad (\sqrt[6]{2})_{135^\circ} \, , \quad (\sqrt[6]{2})_{257^\circ}](/wikipedia/images/math/a/d/b/adb33551ba73519cab6c3b98e938918b.png)
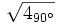 b)
b) ![\sqrt[3]{8_{120^\circ}}](/wikipedia/images/math/0/2/9/02928c662b770c320d65ec6f6ebb988d.png) c)
c) ![\sqrt[5]{5_{270^\circ}}](/wikipedia/images/math/a/a/9/aa96d66344414293e64e280028494f05.png) d)
d) ![\sqrt[4]{6_{120^\circ}}](/wikipedia/images/math/5/b/2/5b29523f5dc1a2d4bbc07a377e06bae8.png)

