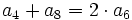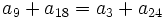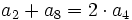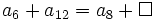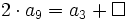Plantilla:Actividades progresiones aritmeticas
De Wikipedia
| Revisión de 10:36 14 sep 2016 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 06:46 10 oct 2016 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 55: | Línea 55: | ||
| |url1=http://matematicasbachiller.com/videos/1-bachillerato/matematicas-de-primero-de-bachillerato/04-sucesiones-aritmeticas-sucesiones-geometricas/0401-cuatro-ejercicios#.VCak8fl_u2E | |url1=http://matematicasbachiller.com/videos/1-bachillerato/matematicas-de-primero-de-bachillerato/04-sucesiones-aritmeticas-sucesiones-geometricas/0401-cuatro-ejercicios#.VCak8fl_u2E | ||
| |sinopsis=Sea <math>\{ a_n \} \;</math> una progresión aritmética de diferencia d. Determina: | |sinopsis=Sea <math>\{ a_n \} \;</math> una progresión aritmética de diferencia d. Determina: | ||
| - | #<math>S_{13} \;</math> sabiendo que <math>a_1=4 \;</math> y d=2. | + | #<math>S_{13} \;</math> sabiendo que <math>a_1=4 \;</math> y <math>d=2\;</math>. |
| - | #<math>S_{15} \;</math> sabiendo que <math>a_{15}=25 \;</math> y d=2. | + | #<math>S_{15} \;</math> sabiendo que <math>a_{15}=25 \;</math> y <math>d=2\;</math>. |
| - | #<math>S_{20} \;</math> sabiendo que <math>a_{12}=18 \;</math> y d=3. | + | #<math>S_{20} \;</math> sabiendo que <math>a_{12}=18 \;</math> y <math>d=3\;</math>. |
| - | #k sabiendo que <math>a_1=2 \;</math>, d=6 y <math>S_k=70 \;</math>. | + | #k sabiendo que <math>a_1=2 \;</math>, <math>d=6\;</math> y <math>S_k=70 \;</math>. |
| }} | }} | ||
| {{p}} | {{p}} | ||
Revisión de 06:46 10 oct 2016
|
Actividad: Progresiones aritméticas Dada la sucesión {1, 4, 7, 10, 13, 16, ...}: a) Halla el término general. b) Halla el término 20. c) Halla la suma de los 20 primeros términos. d) Halla la suma de los términos del 8 al 15. d) Halla la suma de los términos del p al q. Solución: Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones: Tras obtener la solución del apartado a), utilízala para hallas las soluciones de los demás apartados. a) {1, 4, 7, 10, 13, 16, ...} b) {3n-2} for n=20 c) sum {3n-2} for n=1 to 20 d) sum {3n-2} for n=8 to 15 e) sum {3n-2} for n=p to q |
Sea 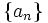 una progresión aritmética de diferencia "d":
una progresión aritmética de diferencia "d":
- Determina
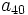 sabiendo que
sabiendo que  y d=3.
y d=3.
- Determina d sabiendo que
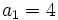 y
y 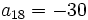 .
.
- Determina n sabiendo que
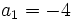 y
y 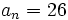 y d=3.
y d=3.
- Determina d,
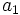 y
y  sabiendo que
sabiendo que 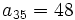 y
y 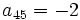 .
.
- Determina
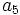 y
y 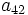 sabiendo que
sabiendo que 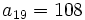 y d=4.
y d=4.
Sea 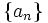 una progresión aritmética. ¿Son ciertas las siguientes afirmaciones?
una progresión aritmética. ¿Son ciertas las siguientes afirmaciones?
Completa las siguientes igualdades:
- Sea
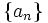 una progresión aritmética. Halla
una progresión aritmética. Halla 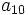 sabiendo que
sabiendo que 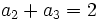 y
y 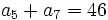 .
.
- Si las longitudes de los lados de un triángulo rectángulo están en progresión aritmética, determina el perímetro sabiendo que la hipotenusa mide 30 m.
- Determina tres números en progresión aritmética de modo que su suma sea 12 y la suma de sus cuadrados sea 16.
- Determina los lados de un triángulo rectángulo sabiendo que están en progresión aritmética de diferencia 7.
Sea 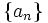 una progresión aritmética de diferencia d. Determina:
una progresión aritmética de diferencia d. Determina:
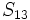 sabiendo que
sabiendo que 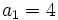 y
y 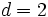 .
.
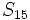 sabiendo que
sabiendo que 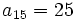 y
y 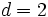 .
.
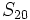 sabiendo que
sabiendo que 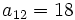 y
y 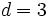 .
.
- k sabiendo que
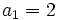 ,
, 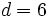 y
y 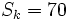 .
.
Sea 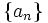 una progresión aritmética de diferencia d. Determina:
una progresión aritmética de diferencia d. Determina:
- d sabiendo que
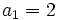 y
y 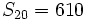
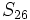 sabiendo que
sabiendo que 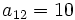 y
y 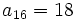 .
.
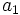 sabiendo que d=3 y
sabiendo que d=3 y 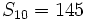 .
.
- k sabiendo que
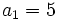 ,
, 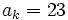 y
y 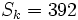 .
.
- La suma de los n primeros términos de la sucesión 3, 7, 11, ... es 210. Halla n.
- La suma de los 6 primeros términos de una progresión aritmética es 36, siendo
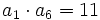 . Determina el término general de la progresión.
. Determina el término general de la progresión.
|
Problema: Progresiones aritméticas Al excavar tierra para hacer un túnel se pagan 700€ por el primer metro y 95€ de aumento por cada metro sucesivo. a) ¿Cuánto se pagará por el décimo metro excavado? b) Calcular el total abonado por los 10 metros excavados.Solución: 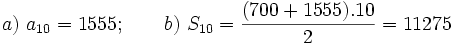 |