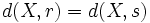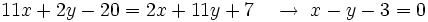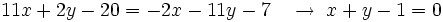Lugares geométricos (1ºBach)
De Wikipedia
| Revisión de 11:27 16 oct 2016 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 11:29 16 oct 2016 Coordinador (Discusión | contribuciones) (→Bisectriz del ángulo entre dos rectas) Ir a siguiente diferencia → |
||
| Línea 74: | Línea 74: | ||
| {{p}} | {{p}} | ||
| - | {{Teorema|titulo=Proposición|enunciado=La bisectriz del ángulo entre dos rectas es un par de rectas perpendiculares|demo=}} | + | {{Teorema|titulo=Proposición|enunciado=La bisectriz del ángulo entre dos rectas son un par de rectas perpendiculares|demo=}} |
| {{p}} | {{p}} | ||
| {{Ejemplo|titulo=Ejemplo: ''Bisectriz del ángulo entre dos rectas''|enunciado=Halla las ecuaciones de las bisectrices del ángulo que forman las rectas <math>r: \, 11x+2y-20=0</math> y <math>s: \, 2x+11y+7=0</math>, y la represéntalas gráficamente. | {{Ejemplo|titulo=Ejemplo: ''Bisectriz del ángulo entre dos rectas''|enunciado=Halla las ecuaciones de las bisectrices del ángulo que forman las rectas <math>r: \, 11x+2y-20=0</math> y <math>s: \, 2x+11y+7=0</math>, y la represéntalas gráficamente. | ||
Revisión de 11:29 16 oct 2016
| Enlaces internos | Para repasar o ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadoras |
Lugar geométrico
Se llama lugar geométrico a un conjunto de puntos que cumplen una cierta propiedad.
Vamos a estudiar a continuación algunos lugares geométricos como la mediatriz de un segmento o la bisectriz de un ángulo. En cada caso buscaremos una ecuación que describa a dicho lugar geométrico.
Mediatriz de un segmento
La mediatriz de un segmento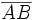 
, es el lugar geométrico de los puntos 
, que equidistan de los extremos 
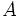y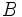 
.
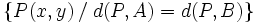
Proposición
La mediatriz de un segmento es una recta.
Para hallar la ecuación de la mediatriz AB, siendo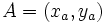 
y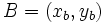 
tenemos que hallar la ecuación del lugar geométrico
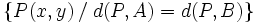
Para ello escribiremos la fórmula de la distancia entre dos puntos:
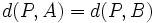
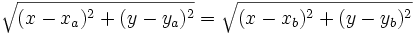
Elevando ambos miembros al cuadrado, desarrollando los cuadrados de los binomios y simplificando, comprueba que queda la ecuación:
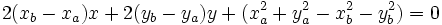
Ejemplo: Mediatriz de un segmento
Halla la ecuación de la mediatriz del segmento de extremos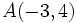 
y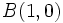 
y represéntala gráficamente.
Para hallar la ecuación del lugar geométrico
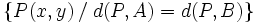
escribiremos la fórmula de la distancia entre dos puntos:
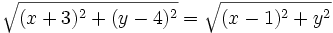
Elevando ambos miembros al cuadrado, desarrollando los cuadrados de los binomios y simplificando, comprueba que queda la ecuación:
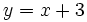
Por tanto, la mediatriz del segmento es una recta.
Bisectriz del ángulo entre dos rectas
La bisectriz del ángulo que forman las rectas 
y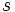 
, es el lugar geométrico de los puntos , que equidistan de los lados y .
|
|
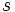Proposición
La bisectriz del ángulo entre dos rectas son un par de rectas perpendiculares
Ejemplo: Bisectriz del ángulo entre dos rectas
Halla las ecuaciones de las bisectrices del ángulo que forman las rectas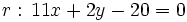 
y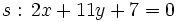 
, y la represéntalas gráficamente.
Para hallar la ecuación del lugar geométrico
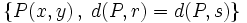
escribiremos la fórmula de la distancia de un punto a una recta:
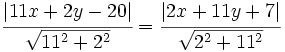
De aquí salen dos ecuaciones, ya que si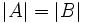 
, se puede dar 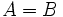que 
o que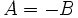 
Así, las dos ecuaciones resultantes son:
o bien
Por tanto, dos rectas, al determinar dos ángulos, dan lugar a dos bisectrices, que son rectas perpendiculares. En la siguiente escena tienes representadas en rojo la segunda y en gris la primera.
Bisectrices del ángulo entre dos rectas (5´29") Sinopsis:Las bisectrices de los ángulos determinados por dos rectas están formadas por los puntos que equidistan de ambas rectas.
Ejercicio (7´50") Sinopsis:Determina la bisectriz del ángulo entre dos rectas dadas en ecuaciones generales.
Ejercicio (Incentro de un triángulo) (9´37") Sinopsis:Determinamos el "incentro" de un triángulo de vértices conocidos. Cae millones de veces todos los años en examen. No es admisible dejarlo escapar.
