Plantilla:Relacion de divisibilidad
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 10:06 20 oct 2016 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 10:07 20 oct 2016 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 4: | Línea 4: | ||
| {{p}} | {{p}} | ||
| {{Ejemplo_simple|titulo=Ejemplos:|contenido= | {{Ejemplo_simple|titulo=Ejemplos:|contenido= | ||
| - | *Un listón de 60 cm se puede partir, exactamente, en trozos de 15 cm, porque la división 60:15 es exacta (cociente=4; resto=0). Por tanto, 60 y 15 están emparentados por la relación de divisibilidad. | + | *Un listón de 60 cm se puede partir, exactamente, en trozos de 15 cm, porque la división 60:15 es exacta (cociente=4; resto=0). Por tanto, 60 y 15 '''están emparentados''' por la relación de divisibilidad. |
| - | *Un listón de 60 cm no se puede partir, exactamente, en trozos de 25 cm, porque la división 60:25 no es exacta (cociente=2; resto=10). Así, 60 y 25 no están emparentados por la relación de divisibilidad. | + | *Un listón de 60 cm no se puede partir, exactamente, en trozos de 25 cm, porque la división 60:25 no es exacta (cociente=2; resto=10). Así, 60 y 25 '''no están emparentados''' por la relación de divisibilidad. |
| }} | }} | ||
| {{p}} | {{p}} | ||
Revisión de 10:07 20 oct 2016
Dos números 
y 
están emparentados por la relación de divisibilidad cuando la división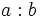 
es exacta.
- Un listón de 60 cm se puede partir, exactamente, en trozos de 15 cm, porque la división 60:15 es exacta (cociente=4; resto=0). Por tanto, 60 y 15 están emparentados por la relación de divisibilidad.
- Un listón de 60 cm no se puede partir, exactamente, en trozos de 25 cm, porque la división 60:25 no es exacta (cociente=2; resto=10). Así, 60 y 25 no están emparentados por la relación de divisibilidad.
Exposición: Relación de divisibilidad Descripción: Actividades: Relación de divisibilidad Descripción: 
