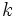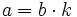Plantilla:Def Multiplo y divisor
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 10:09 20 oct 2016 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 10:10 20 oct 2016 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 11: | Línea 11: | ||
| {{p}} | {{p}} | ||
| {{Teorema|titulo=Proposición|enunciado= | {{Teorema|titulo=Proposición|enunciado= | ||
| - | :Si {{Sube|porcentaje=+10%|contenido=<math>a\;\!</math>}} es multiplo de {{Sube|porcentaje=+15%|contenido=<math>b\,</math>}} , entonces existe un número natural {{Sube|porcentaje=+15%|contenido=<math>k\;\!</math>}} tal que {{Sube|porcentaje=+20%|contenido=<math>a=b \cdot k</math>}}. | + | Si {{Sube|porcentaje=+10%|contenido=<math>a\;\!</math>}} es multiplo de {{Sube|porcentaje=+15%|contenido=<math>b\,</math>}} , entonces existe un número natural {{Sube|porcentaje=+15%|contenido=<math>k\;\!</math>}} tal que {{Sube|porcentaje=+20%|contenido=<math>a=b \cdot k</math>}}. |
| |demo=En efecto, si ''a'' es multiplo de ''b'', entonces la división ''a:b'' es exacta. Si llamamos ''k'' al cociente, se cumple que {{Sube|porcentaje=+20%|contenido=<math>a=b \cdot k</math>}}.}} | |demo=En efecto, si ''a'' es multiplo de ''b'', entonces la división ''a:b'' es exacta. Si llamamos ''k'' al cociente, se cumple que {{Sube|porcentaje=+20%|contenido=<math>a=b \cdot k</math>}}.}} | ||
| {{p}} | {{p}} | ||
Revisión de 10:10 20 oct 2016
Si  y
y 
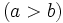 están emparentados por la relación de divisibilidad, es decir,
están emparentados por la relación de divisibilidad, es decir, 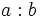 es exacta, entonces decimos que:
es exacta, entonces decimos que:
 es multiplo
es multiplo  y lo expresaremos simbólicamente:
y lo expresaremos simbólicamente: 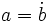 .
.
 es divisor de
es divisor de  y lo expresaremos simbólicamente:
y lo expresaremos simbólicamente: 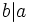 .
.
- La división 60:15=4 es exacta. Entonces 60 es un múltiplo de 15
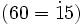 y 15 es un divisor de 60
y 15 es un divisor de 60 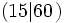 .
.
- Fíjate que 4 también es divisor de 60 porque la división 60:4=15 es también exacta. Por tanto, los divisores siempre van por parejas.