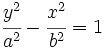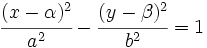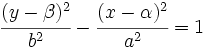La hipérbola (1ºBach)
De Wikipedia
| Revisión de 17:06 20 oct 2016 Coordinador (Discusión | contribuciones) (→Construcciones de la hipérbola) ← Ir a diferencia anterior |
Revisión de 17:07 20 oct 2016 Coordinador (Discusión | contribuciones) (→Construcciones de la hipérbola) Ir a siguiente diferencia → |
||
| Línea 153: | Línea 153: | ||
| {{Geogebra_enlace | {{Geogebra_enlace | ||
| |descripcion=En esta escena podrás ver como construye una hipérbola usando la definición de hipérbola como lugar geométrico. | |descripcion=En esta escena podrás ver como construye una hipérbola usando la definición de hipérbola como lugar geométrico. | ||
| - | |enlace=[https://ggbm.at/ukt4c5TW Trazado de la hipérbola] | + | |enlace=[https://ggbm.at/ukt4c5TW Trazado de la hipérbola a partir de la definición] |
| }} | }} | ||
| {{p}} | {{p}} | ||
Revisión de 17:07 20 oct 2016
| Enlaces internos | Para repasar o ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadoras |
Tabla de contenidos |
La hipérbola
Dados dos puntos 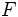 y
y 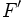 llamados focos, y una distancia
llamados focos, y una distancia  , llamada constante de la hipérbola (
, llamada constante de la hipérbola (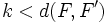 ), se llama hipérbola al lugar geométrico de los puntos
), se llama hipérbola al lugar geométrico de los puntos  del plano cuya diferencia de distancias a los focos es, en valor absoluto, igual a
del plano cuya diferencia de distancias a los focos es, en valor absoluto, igual a  :
:
|
|
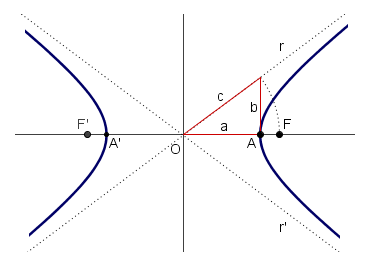
Elementos de la hipérbola
Una una hipérbola de focos
Propiedades
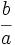 y y 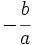 Demostración:
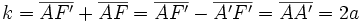
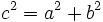 Por ser
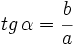 |
Excentricidad de la hipérbola
La excentricidad de la hipérbola es el cociente entre la distancia focal y el eje:
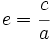
Propiedades
En una hipérbola 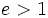 .
.
Como la hipotenusa del triángulo rectángulo es mayor que los catetos, tenemos que
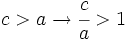
En la siguiente escena vamos a ver como se ve afectada la hipérbola si modificamos su excentricidad.
Ecuaciones de la hipérbola
Ecuación reducida de la hipérbola
Ecuación reducida de la hipérbola
- La ecuación de una hipérbola con semieje
 , con centro en el origen de coordenadas y focos en el eje de abscisas es:
, con centro en el origen de coordenadas y focos en el eje de abscisas es:
|
|
Sean  y
y 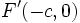 los focos de la elipse. Cualquier punto P(x,y) de la misma cumple:
los focos de la elipse. Cualquier punto P(x,y) de la misma cumple:
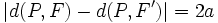
Sustituyendo las distancias por su fórmula matemática, y contemplando la posibilidad del doble signo que surge de suprimir el valor absoluto:
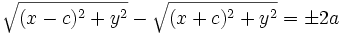
Pasamos la segunda raíz al segundo miembro:
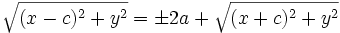
Se elevan al cuadrado ambos miebros y se simplifica:
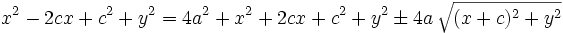
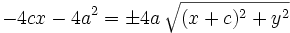
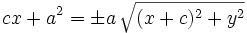
Se elevan al cuadrado los dos miembros:
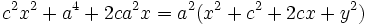
Reordenando y agrupando términos:
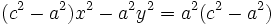
Teniendo en cuenta que 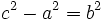 :
:
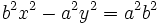
Dividiendo la expresión por 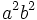 :
:
se obtiene la cuación buscada:
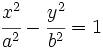
En la siguiente escena vamos a calcular la ecuación reducida de la hipérbola con semieje 4 y semidistancia focal 5.
Ecuación de la hipérbola con los focos en el eje Y
Ecuación de la hipérbola con los focos en el eje Y
- La ecuación de una hipérbola con semieje
 , con centro en el origen de coordenadas y focos en el eje de ordenadas es:
, con centro en el origen de coordenadas y focos en el eje de ordenadas es:
|
|
Ecuación de la hipérbola con el centro desplazado del origen de coordenadas
Ecuación de la hipérbola con el centro desplazado del origen
- La ecuación de una elipse con semieje
 y centro
y centro 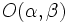 es:
es:
- Si el eje FF' es paralelo al eje X:
|
|
- Si el eje FF' es perpendicular al eje X:
|
|
En la siguiente escena vamos a calcular la ecuación de la hipérbola de centro O(-3,1), semieje a=3 y semidistancia focal c=5.
En la siguiente escena vamos a calcular la ecuación de la hipérbola con eje focal vertical de centro O(3,-1), a=2 y b=3.
Construcciones de la hipérbola
En esta escena podrás ver como construye una hipérbola usando la definición de hipérbola como lugar geométrico.
En esta escena podrás ver como construye una hipérbola como envolvente.
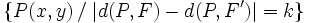
 y
y 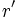
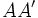

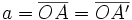
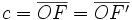
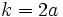 (constante de la hipérbola)
(constante de la hipérbola)
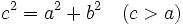
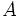 un punto de la hipérbola:
un punto de la hipérbola:
 y
y 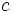 , tenemos
, tenemos
 .
.