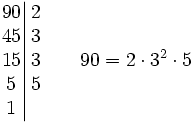Plantilla:Descomposicion en factores
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 07:06 6 sep 2016 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión actual Coordinador (Discusión | contribuciones) |
||
| Línea 1: | Línea 1: | ||
| - | {{Caja_Amarilla|texto=Cualquier número podemos expresarlo como producto de potencias de números primos. A esto se le llama '''descomposición factorial''' de un número.}} | + | {{Caja_Amarilla|texto= Se le llama '''descomposición factorial''' o '''factorización''' de un número, a su expresión como producto de potencias de números primos.}} |
| {{p}} | {{p}} | ||
| - | Para descomponer en factores primos un número: | + | {{Teorema|titulo=Descomposición en factores primos |
| + | |enunciado= | ||
| + | Cualquier número puede expresarse como producto de potencias de números primos. | ||
| - | * Lo dividimos por el primer número primo que podamos. | + | |demo=El procedimiento es el siguiente: |
| - | * El cociente que haya resultado lo colocamos bajo el número. | + | |
| - | * Si podemos seguimos dividiendo sucesivamente ese cociente por el mismo número primo. | + | * Lo dividimos por el menor número primo que podamos. |
| - | * Cuando no podamos hacer la división por ese número primo lo hacemos por el siguiente primo que se pueda. | + | * El cociente que haya resultado lo colocamos debajo del número. |
| + | * Si podemos, seguimos dividiendo sucesivamente ese cociente por el mismo número primo. | ||
| + | * Cuando no podamos hacer la división por ese número primo, lo hacemos por el siguiente primo que se pueda. | ||
| * Así sucesivamente hasta que el cociente final sea 1. | * Así sucesivamente hasta que el cociente final sea 1. | ||
| + | * El producto de todos los números primos por los que hemos ido dividiendo constituyen la descomposición factorial del número. | ||
| + | }} | ||
| + | {{p}} | ||
| + | {{Ejemplo_simple | ||
| + | |titulo= | ||
| + | Ejemplo: | ||
| + | |contenido= | ||
| + | Halla la descomposición factorial de 90. | ||
| + | ---- | ||
| + | '''Solución:''' | ||
| + | |||
| + | Dividimos 90 entre el primer número primo por el que sea divisible. En este caso, por 2. (90:2=45) | ||
| + | A continuación, procedemos a dividir 45, cociente de la anterior división, de igual forma. (45:3=15) | ||
| + | Así sucesivamente hasta obtener 1 en el cociente (15:3=5; 5:5=1) | ||
| + | |||
| + | Los cocientes 2, 3, 3 y 5 son los factores que descomponen a 90. | ||
| + | |||
| + | <center><math>\left . \begin{matrix} 90 \\ 45 \\ 15 \\ 5 \\ 1 \end{matrix} \right |\begin{matrix} 2 \\ 3 \\ 3 \\ 5 \\ \; \end{matrix} \qquad 90=2 \cdot3^2 \cdot 5</math></center> | ||
| + | }} | ||
Revisión actual
Se le llama descomposición factorial o factorización de un número, a su expresión como producto de potencias de números primos.
Descomposición en factores primos
Cualquier número puede expresarse como producto de potencias de números primos.
Demostración:
El procedimiento es el siguiente:
- Lo dividimos por el menor número primo que podamos.
- El cociente que haya resultado lo colocamos debajo del número.
- Si podemos, seguimos dividiendo sucesivamente ese cociente por el mismo número primo.
- Cuando no podamos hacer la división por ese número primo, lo hacemos por el siguiente primo que se pueda.
- Así sucesivamente hasta que el cociente final sea 1.
- El producto de todos los números primos por los que hemos ido dividiendo constituyen la descomposición factorial del número.
Halla la descomposición factorial de 90.
Solución:
Dividimos 90 entre el primer número primo por el que sea divisible. En este caso, por 2. (90:2=45) A continuación, procedemos a dividir 45, cociente de la anterior división, de igual forma. (45:3=15) Así sucesivamente hasta obtener 1 en el cociente (15:3=5; 5:5=1)
Los cocientes 2, 3, 3 y 5 son los factores que descomponen a 90.