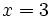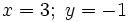Plantilla:Método de reducción
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 11:54 1 nov 2016 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 11:56 1 nov 2016 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 1: | Línea 1: | ||
| {{Teorema_sin_demo|titulo=Procedimiento|enunciado= | {{Teorema_sin_demo|titulo=Procedimiento|enunciado= | ||
| Para resolver un sistema por el método de '''reducción''' se siguen los siguientes pasos: | Para resolver un sistema por el método de '''reducción''' se siguen los siguientes pasos: | ||
| - | #Se obtiene un sistema equivalente al de partida, multiplicando las dos ecuaciones por números apropiados de manera que una de las incógnitas quede con coeficentes opuestos en ambas ecuaciones. | + | #Se obtiene un sistema equivalente al de partida, multiplicando las dos ecuaciones por números apropiados, de manera que una de las incógnitas quede con coeficentes opuestos en ambas ecuaciones. |
| - | #Se suman ambas ecuaciones, desapareciendo así una de las incógnitas. | + | #Se suman las ecuaciones del nuevo sistema, desapareciendo así la incógnita con coeficientes opuestos. |
| #Se resuelve la ecuación obtenida en (2), averiguando así una de las incógnitas del sistema. | #Se resuelve la ecuación obtenida en (2), averiguando así una de las incógnitas del sistema. | ||
| #El valor obtenido en (3) se sustitute en una de las dos ecuaciones del sistema de partida, averiguando así el valor de la incógnita que faltaba, y, por tanto, resolviendo el sistema. | #El valor obtenido en (3) se sustitute en una de las dos ecuaciones del sistema de partida, averiguando así el valor de la incógnita que faltaba, y, por tanto, resolviendo el sistema. | ||
| - | |||
| - | El método de '''reducción''' consiste en obtener ecuaciones equivalentes a las de partida, de manera que al sumarlas, se obtenga una ecuación en la que se ha eliminado una de las incógnitas. Así, nos queda una ecuación con una sola incógnita, que se resuelve, permitiendo averiguar dicha incógnita. Finalmente, el valor de la otra incógnita se obtiene sustituyendo el valor obtenido. | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
Revisión de 11:56 1 nov 2016
Procedimiento
Para resolver un sistema por el método de reducción se siguen los siguientes pasos:
- Se obtiene un sistema equivalente al de partida, multiplicando las dos ecuaciones por números apropiados, de manera que una de las incógnitas quede con coeficentes opuestos en ambas ecuaciones.
- Se suman las ecuaciones del nuevo sistema, desapareciendo así la incógnita con coeficientes opuestos.
- Se resuelve la ecuación obtenida en (2), averiguando así una de las incógnitas del sistema.
- El valor obtenido en (3) se sustitute en una de las dos ecuaciones del sistema de partida, averiguando así el valor de la incógnita que faltaba, y, por tanto, resolviendo el sistema.
Ejemplo: Método de reducción
Resuelve por el método de reducción el siguiente sistema:
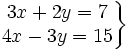
Solución:
- Multiplicamos la primera ecuación por 4 y la segunda por (-3)
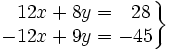
- Sumamos miembro a miembro las dos ecuaciones:
|
|
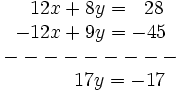
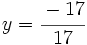
- Sustituimos el valor
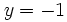en cualquiera de las dos ecuaciones del sistema de partida, por ejemplo en la primera: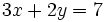 
|
|
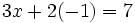
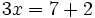
- Así, la solución del sistema es:
|
|
