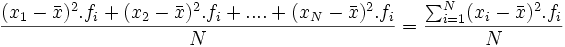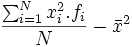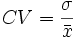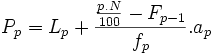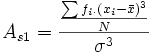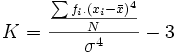Análisis descriptivo
De Wikipedia
| Revisión de 11:26 25 jun 2007 Juanmf (Discusión | contribuciones) (→Parámetros de posición) ← Ir a diferencia anterior |
Revisión actual Coordinador (Discusión | contribuciones) (→Actividades) |
||
| Línea 1: | Línea 1: | ||
| + | {{Menú Estadistica 2BH | ||
| + | |ir= | ||
| + | |repasar= | ||
| + | |ampliar= | ||
| + | |enlaces= | ||
| + | }} | ||
| =Tablas= | =Tablas= | ||
| ==Tablas estadísticas== | ==Tablas estadísticas== | ||
| Línea 130: | Línea 136: | ||
| {{p}} | {{p}} | ||
| <center><iframe> | <center><iframe> | ||
| - | url=http://maralboran.ath.cx/web_ma/wiki_Estadistica/descriptiva/variables/frecuencias_discreta_est.htm | + | url=http://maralboran.org/web_ma/wiki_Estadistica/descriptiva/variables/frecuencias_discreta_est.htm |
| width=100% | width=100% | ||
| height=730 | height=730 | ||
| Línea 142: | Línea 148: | ||
| {{p}} | {{p}} | ||
| <center><iframe> | <center><iframe> | ||
| - | url=http://maralboran.ath.cx/web_ma/wiki_Estadistica/descriptiva/variables/frecuencias_continua_est.htm | + | url=http://maralboran.org/web_ma/wiki_Estadistica/descriptiva/variables/frecuencias_continua_est.htm |
| width=100% | width=100% | ||
| height=730 | height=730 | ||
| Línea 166: | Línea 172: | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| + | |||
| =Gráficos= | =Gráficos= | ||
| Una vez construida la tabla de frecuencias, vamos a representar mediante distintos gráficos el estudio realizado. Entre los gráficos más utilizado podemos destacar: | Una vez construida la tabla de frecuencias, vamos a representar mediante distintos gráficos el estudio realizado. Entre los gráficos más utilizado podemos destacar: | ||
| Línea 252: | Línea 259: | ||
| Para calcular la media aritmética hacemos: | Para calcular la media aritmética hacemos: | ||
| <center> | <center> | ||
| - | <math> \bar x\ </math> = <math>\frac{x_1 + x_2 + ....+x_N} {N}={\sum_{i=1}^N x_i \over N} </math></center> | + | {{Caja|contenido=<math> \bar x\ </math> = <math>\frac{x_1 + x_2 + ....+x_N} {N}={\sum_{i=1}^N x_i \over N} </math>}} |
| + | </center> | ||
| donde <math>N = num.\ total\ de\ individuos = \sum_{i=1}^N f_i</math>. | donde <math>N = num.\ total\ de\ individuos = \sum_{i=1}^N f_i</math>. | ||
| Línea 259: | Línea 267: | ||
| Sin embargo, podemos observar que aparecen datos repetidos y que en un estudio estadístico tenemos los datos agrupados en una tabla en la que aparecen las frecuencias. Por tanto, podemos simplificar el cálculo de la media aritmética con la fórmula: | Sin embargo, podemos observar que aparecen datos repetidos y que en un estudio estadístico tenemos los datos agrupados en una tabla en la que aparecen las frecuencias. Por tanto, podemos simplificar el cálculo de la media aritmética con la fórmula: | ||
| <center> | <center> | ||
| - | <math> \bar x\ </math> = <math>\frac{x_1.f_1 + x_2.f_2 + ....+x_N.f_N} {N}={\sum_{i=1}^N x_i.f_i \over N} </math> | + | {{Caja|contenido=<math> \bar x\ </math> = <math>\frac{x_1.f_1 + x_2.f_2 + ....+x_N.f_N} {N}={\sum_{i=1}^N x_i.f_i \over N} </math>}} |
| </center> | </center> | ||
| }} | }} | ||
| Línea 309: | Línea 317: | ||
| Sin embargo si la variable es '''continua''' la mayor frecuencia absoluta corresponde a un intervalo, del que decimos que es el '''intervalo modal'''. Pero si queremos calcular un único valor de la variable para la moda, aplicamos la siguiente fórmula: | Sin embargo si la variable es '''continua''' la mayor frecuencia absoluta corresponde a un intervalo, del que decimos que es el '''intervalo modal'''. Pero si queremos calcular un único valor de la variable para la moda, aplicamos la siguiente fórmula: | ||
| <center> | <center> | ||
| - | <math>Mo = L_i + {f_{Mo}-f_{Mo-1} / over {(f_{Mo}-f_{Mo-1}+ f_{Mo}-f_{Mo+1}}.a_i</math> | + | {{Caja|contenido=<math> Mo = L_i + {f_{Mo+1} \over f_{Mo+1}+ f_{Mo-1}}.a_i </math> |
| - | + | }} | |
| </center> | </center> | ||
| - | en la que Li representa el límite inferior del intervalo modal, c es la amplitud del intervalo y fMo, fMo-1 y fMo+1 son las frecuencias del intervalo modal, el anterior y el posterior. | + | en la que <math> L_i </math> representa el límite inferior del intervalo modal, <math> a_i </math> es la amplitud del intervalo.<br> <math>f_{Mo-1}</math> y <math>f_{Mo+1}</math> son las frecuencias del intervalo modal, el anterior y el posterior. |
| Línea 323: | Línea 331: | ||
| <center><iframe> | <center><iframe> | ||
| url=http://maralboran.ath.cx/web_ma/wiki_Estadistica/descriptiva/variables/moda_discreta_est.htm | url=http://maralboran.ath.cx/web_ma/wiki_Estadistica/descriptiva/variables/moda_discreta_est.htm | ||
| + | width=100% | ||
| + | height=600 | ||
| + | name=myframe | ||
| + | </iframe></center>}} | ||
| + | {{ai_cuerpo | ||
| + | |enunciado='''Actividad 2'''. Variable continua. | ||
| + | |actividad= Calcula en tu cuaderno la moda para el ejemplo de la estatura: 1.59, 1.75, 1.71, 1.85, 1.64, 1.62, 1.66, 1.60, 1.63, 1.76, 1.66, utilizando los mismos intervalos que hayas construido antes. Una vez que la tienes en tu cuaderno, calcúlala con la escena y compara los resultados. | ||
| + | <center><iframe> | ||
| + | url=http://maralboran.ath.cx/web_ma/wiki_Estadistica/descriptiva/variables/moda_continua_est.htm | ||
| width=100% | width=100% | ||
| height=600 | height=600 | ||
| Línea 335: | Línea 352: | ||
| :a) Modifica las frecuencias y observa como puede variar el valor de la moda. | :a) Modifica las frecuencias y observa como puede variar el valor de la moda. | ||
| :b) ¿Puede una distribución estadística tener más de una moda? ¿Pueden ser todos los valores de la variable? | :b) ¿Puede una distribución estadística tener más de una moda? ¿Pueden ser todos los valores de la variable? | ||
| + | '''Actividad 2:''' | ||
| + | |||
| + | En este caso de la estatura, se ha calculado la moda utilizando intervalos, pero como tenemos pocos valores de la variable, si los observamos, ¿cuál es la moda? ¿Coincide el resultado? ¿Por qué ? | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| Línea 341: | Línea 361: | ||
| <div style="background: white; border: 2px solid Gold;border-left: 4px solid Gold;border-bottom: 4px solid Gold; padding:.75em;"> | <div style="background: white; border: 2px solid Gold;border-left: 4px solid Gold;border-bottom: 4px solid Gold; padding:.75em;"> | ||
| Si ordenamos todos los valores de la variable de menor a mayor, se define la '''mediana''' como el valor de la variable que está en el centro. Se representa por Me. Aquí tenemos que comprender que si hay un número impar de valores, habrá un sólo valor central; mientras que si hay un número par de valores habrá dos valores centrales. | Si ordenamos todos los valores de la variable de menor a mayor, se define la '''mediana''' como el valor de la variable que está en el centro. Se representa por Me. Aquí tenemos que comprender que si hay un número impar de valores, habrá un sólo valor central; mientras que si hay un número par de valores habrá dos valores centrales. | ||
| + | Si la variable es '''discreta''' y el número de datos es par, la mediana será la media aritmética de los dos valores centrales. | ||
| + | |||
| + | Si la variable es '''continua''', no distinguiremos si el número de datos es par o impar, tendremos un intervalo para la mediana. Igual que se ha hecho con la moda podemos suponer que los datos se distribuyen uniformemente en los intervalos y calcular la mediana con la siguiente fórmula: | ||
| + | <center> | ||
| + | {{Caja|contenido=<math> Me = L_{Me}+{{N \over 2}-F_{Me-1} \over f_{Me}}.a_{Me} </math>}} | ||
| + | </center> | ||
| + | en la que <math> L_{Me} </math> representa el límite inferior del intervalo de la mediana, <math> a_{Me} </math> es la amplitud del intervalo, <math>F_{Me-1}</math> la frecuencia acumulada anterior, y <math>f_{Me}</math> frecuencia absoluta del intervalo. | ||
| </div> | </div> | ||
| {{p}} | {{p}} | ||
| Línea 353: | Línea 380: | ||
| name=myframe | name=myframe | ||
| </iframe></center>}} | </iframe></center>}} | ||
| + | {{ai_cuerpo | ||
| + | |enunciado='''Actividad 2'''. Variable continua. | ||
| + | |actividad= Calcula en tu cuaderno la mediana para el ejemplo de la estatura: 1.59, 1.75, 1.71, 1.85, 1.64, 1.62, 1.66, 1.60, 1.63, 1.76, 1.66, utilizando los mismos intervalos que hayas construido antes.Una vez que la tienes en tu cuaderno, calcúlala con la escena y compara los resultados. | ||
| + | <center><iframe> | ||
| + | url=http://maralboran.ath.cx/web_ma/wiki_Estadistica/descriptiva/variables/mediana_continua_est.htm | ||
| + | width=100% | ||
| + | height=600 | ||
| + | name=myframe | ||
| + | </iframe></center>}} | ||
| + | |||
| }} | }} | ||
| {{ejercicio | {{ejercicio | ||
| Línea 360: | Línea 397: | ||
| :a) Modifica las frecuencias y observa como puede variar el valor de la mediana. | :a) Modifica las frecuencias y observa como puede variar el valor de la mediana. | ||
| :b) ¿Cuál es el valor menor que puede tomar? ¿Y el mayor? | :b) ¿Cuál es el valor menor que puede tomar? ¿Y el mayor? | ||
| + | '''Actividad 2:''' | ||
| + | |||
| + | En este caso de la estatura, se ha calculado la mediana utilizando intervalos, pero como tenemos pocos valores de la variable, ordénalos de menor a mayor y calcula el resultado, ¿cuál es la mediana? ¿Coincide el resultado? ¿Por qué ? | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| Línea 372: | Línea 412: | ||
| Se define la '''varianza''' como la media aritmética de los cuadrados de las desviaciones respecto de la media. Es decir: | Se define la '''varianza''' como la media aritmética de los cuadrados de las desviaciones respecto de la media. Es decir: | ||
| <center> | <center> | ||
| - | <math> \sigma^2\ </math> = <math>\frac{(x_1 - \bar x)^2.f_i + (x_2 - \bar x)^2.f_i + ....+(x_N - \bar x)^2.f_i} {N}={\sum_{i=1}^N (x_i - \bar x)^2.f_i \over N} </math> | + | {{Caja|contenido=<math> \sigma^2\ </math> = <math>\frac{(x_1 - \bar x)^2.f_i + (x_2 - \bar x)^2.f_i + ....+(x_N - \bar x)^2.f_i} {N}={\sum_{i=1}^N (x_i - \bar x)^2.f_i \over N} </math>}} |
| </center> | </center> | ||
| Se calcula más facilmente, con la siguiente fórmula equivalente: | Se calcula más facilmente, con la siguiente fórmula equivalente: | ||
| <center> | <center> | ||
| - | <math> \sigma^2\ </math> = <math>{\sum_{i=1}^N x_i^2.f_i \over N} - \bar x^2 </math> | + | {{Caja|contenido=<math> \sigma^2\ </math> = <math>{\sum_{i=1}^N x_i^2.f_i \over N} - \bar x^2 </math>}} |
| </center> | </center> | ||
| Se define la '''desviación típica''' como la raíz cuadrada positiva de la varianza. | Se define la '''desviación típica''' como la raíz cuadrada positiva de la varianza. | ||
| Línea 458: | Línea 498: | ||
| {{Caja_Amarilla|texto='''Coeficiente de variación'''. Si hemos realizado un estudio estadístico en dos poblaciones diferentes, y queremos comparar resultados, no podemos acudir a la desviación típica para ver la mayor o menor homogeneidad de los datos, sino a otro parámetro nuevo, llamado coeficiente de variación y que se define como el cociente entre la desviación típica y la media. | {{Caja_Amarilla|texto='''Coeficiente de variación'''. Si hemos realizado un estudio estadístico en dos poblaciones diferentes, y queremos comparar resultados, no podemos acudir a la desviación típica para ver la mayor o menor homogeneidad de los datos, sino a otro parámetro nuevo, llamado coeficiente de variación y que se define como el cociente entre la desviación típica y la media. | ||
| <center> | <center> | ||
| - | <math> {CV}={\sigma \over \bar x} </math> | + | {{Caja|contenido=<math> {CV}={\sigma \over \bar x} </math>}} |
| </center> | </center> | ||
| }} | }} | ||
| Línea 471: | Línea 511: | ||
| Por tanto, es más homogéneo el conjunto de las vacas. | Por tanto, es más homogéneo el conjunto de las vacas. | ||
| {{p}} | {{p}} | ||
| + | |||
| ==Parámetros de posición== | ==Parámetros de posición== | ||
| {{Caja_Amarilla|texto= | {{Caja_Amarilla|texto= | ||
| Línea 478: | Línea 519: | ||
| :'''Percentiles'''. Son valores que dividen a la población en cien partes iguales. Los representamos por <math>P_n</math>. Evidentemente los percentiles 25, 50 y 75 coinciden con los cuartiles. Y los percentiles 10, 20 , ... , 90 coinciden con los deciles. | :'''Percentiles'''. Son valores que dividen a la población en cien partes iguales. Los representamos por <math>P_n</math>. Evidentemente los percentiles 25, 50 y 75 coinciden con los cuartiles. Y los percentiles 10, 20 , ... , 90 coinciden con los deciles. | ||
| - | }} | ||
| {{p}} | {{p}} | ||
| El cálculo de estos parámetros, tanto para variables discretas como para variables continuas, se hace de forma similar al cálculo de la mediana. | El cálculo de estos parámetros, tanto para variables discretas como para variables continuas, se hace de forma similar al cálculo de la mediana. | ||
| - | Si la '''variable es discreta''', para calcular un percentil, calcularemos el porcentaje de datos que corresponde a dicho percentil, es decir para calcular el percentil de orden "p", calcularemos p·N/100. Si este valor no coincide con ninguna de las frecuencias absolutas acumuladas, cogemos el primer valor de la variable cuya frecuencia absoluta acumulada supera este dato. Pero si este valor coincide con una frecuencia absoluta acumulada, el percentil buscado será la media aritmética entre el valor de la variable correspondiente y el siguiente. | + | Si la '''variable es discreta''', para calcular un percentil, calcularemos el porcentaje de datos que corresponde a dicho percentil, es decir para calcular el percentil de orden "p", calcularemos <math>{p.N \over 100}</math>. Si este valor no coincide con ninguna de las frecuencias absolutas acumuladas, cogemos el primer valor de la variable cuya frecuencia absoluta acumulada supera este dato. Pero si este valor coincide con una frecuencia absoluta acumulada, el percentil buscado será la media aritmética entre el valor de la variable correspondiente y el siguiente. |
| Si la '''variable es continua''' aplicamos la siguiente fórmula muy similar a la utilizada para el cálculo de la mediana: | Si la '''variable es continua''' aplicamos la siguiente fórmula muy similar a la utilizada para el cálculo de la mediana: | ||
| <center> | <center> | ||
| - | <math> P_p = L_p+{{p.N \over 100}-F_{p-1} \over f_p}.a_p </math> | + | {{Caja|contenido=<math> P_p = L_p+{{p.N \over 100}-F_{p-1} \over f_p}.a_p </math>}} |
| </center> | </center> | ||
| + | en la que <math> L_p </math> representa el límite inferior del intervalo del percentil, <math> a_p </math> es la amplitud del intervalo y <math>F_{p-1}</math> la frecuencia acumulada anterior, <math>f_p</math> frecuencia absoluta del intervalo. | ||
| + | }} | ||
| + | {{p}} | ||
| + | {{AI2|titulo=Actividad Interactiva: ''Percentiles''|cuerpo= | ||
| + | {{ai_cuerpo | ||
| + | |enunciado='''Actividad 1'''. Variable discreta. | ||
| + | |actividad= Calcula en tu cuaderno los cuartiles primero y tercero para el ejemplo del número de hermanos: 2, 3, 2, 3, 3, 3, 3, 4, 2, 2, 2.Una vez que los tienes en tu cuaderno, calcúlalos con la escena y compara los resultados. | ||
| + | <center><iframe> | ||
| + | url=http://maralboran.ath.cx/web_ma/wiki_Estadistica/descriptiva/variables/cuartiles_discreta_est.htm | ||
| + | width=100% | ||
| + | height=600 | ||
| + | name=myframe | ||
| + | </iframe></center>}} | ||
| + | {{ai_cuerpo | ||
| + | |enunciado='''Actividad 2'''. Variable continua. | ||
| + | |actividad= Calcula en tu cuaderno los cuartiles primero y tercero para el ejemplo de la estatura: 1.59, 1.75, 1.71, 1.85, 1.64, 1.62, 1.66, 1.60, 1.63, 1.76, 1.66, utilizando los mismos intervalos que hayas construido antes. Una vez que los tienes en tu cuaderno, calcúlalos con la escena y compara los resultados. | ||
| + | <center><iframe> | ||
| + | url=http://maralboran.ath.cx/web_ma/wiki_Estadistica/descriptiva/variables/cuartiles_continua_est.htm | ||
| + | width=100% | ||
| + | height=600 | ||
| + | name=myframe | ||
| + | </iframe></center>}} | ||
| + | }} | ||
| + | {{ejercicio | ||
| + | |titulo=Actividad: ''Percentiles'' | ||
| + | |cuerpo= | ||
| + | '''Actividad 1:''' | ||
| + | |||
| + | Modifica las frecuencias y calcula varios percentiles. | ||
| + | }} | ||
| + | {{p}} | ||
| + | ==Medidas de forma== | ||
| + | ===Coeficiente de asimetría de Fisher=== | ||
| + | {{Caja_Amarilla|texto= | ||
| + | Permite interpretar la forma de la distribución, respecto a ser o no simétrica. | ||
| + | <center> | ||
| + | {{Caja|contenido=<math> A_{s1} = {{\sum f_i.(x_i-\bar x)^3 \over N} \over \sigma^3} </math>}} | ||
| + | {{p}} | ||
| + | [[Imagen:Image2.gif|200px]][[Imagen:Image1.gif|200px]][[Imagen:Image3.gif|200px]] | ||
| + | </center> | ||
| + | ::<math> A_{s1}< 0 \Rightarrow </math> distribución '''asimétrica negativa'''; existe mayor concentración de valores a la izquierda de la media que a su derecha). | ||
| + | |||
| + | ::<math> A_{s1}= 0 \Rightarrow </math> distribución '''simétrica'''; existe la misma concentración de valores a la derecha y a la izquierda de la media). | ||
| + | |||
| + | ::<math> A_{s1}> 0 \Rightarrow </math> distribución '''asimétrica positiva'''; existe mayor concentración de valores a la derecha de la media que a su izquierda) | ||
| + | }} | ||
| + | |||
| + | ===Coeficiente de curtosis=== | ||
| + | {{Caja_Amarilla|texto= | ||
| + | Recibe también el nombre de coeficiente de concentración central, midiendo el grado de aplastamiento o apuntamiento de la gráfica de la distribución de la variable estadística. Una mayor concentración de datos en torno al promedio harán que la forma sea alargada, siendo tanto más plana (o aplastada) cuanto mayor sea la dispersión de los mismos. | ||
| + | <center> | ||
| + | {{Caja|contenido=<math> K = {{\sum f_i.(x_i-\bar x)^4 \over N} \over \sigma^4}-3 </math>}} | ||
| + | </center> | ||
| + | {{p}} | ||
| + | <center> | ||
| + | [[Imagen:Image6.gif|200px]][[Imagen:Image4.gif|200px]][[Imagen:Image5.gif|200px]] | ||
| + | </center> | ||
| + | |||
| + | ::<math>K<0 \Rightarrow </math>Distribución '''platicúrtica''': presenta un reducido grado de concentración alrededor de los valores centrales de la variable. | ||
| + | |||
| + | ::<math>K=0 \Rightarrow </math>Distribución '''mesocúrtica''': presenta un grado de concentración medio alrededor de los valores centrales de la variable (el mismo que presenta una distribución normal). | ||
| + | |||
| + | ::<math>K>0 \Rightarrow </math>Distribución '''leptocúrtica''': presenta un elevado grado de concentración alrededor de los valores centrales de la variable. | ||
| + | |||
| + | }} | ||
Revisión actual
| Ir a | Para repasar | Para ampliar | Enlaces externos |
| Indice Casio | WIRIS Calculadora Descartes |
Tabla de contenidos |
Tablas
Tablas estadísticas
Son utilizadas para organizar los datos. Según el número de observaciones y según el recorrido de la variable estadística, tenemos los siguientes tipos de tablas estadísticas:
Tablas Tipo I
Cuando el tamaño de la muestra y el recorrido (mayor valor menos el valor menor) de la variable son pequeños, por ejemplo si tenemos una muestra de las edades de 5 personas, por lo que no hay que hacer nada especial simplemente anotarlas de manera ordenada en filas o columnas.
Edad de los 5 miembros de una familia:
5, 8, 16, 38, 45
Tablas Tipo II
Cuando el tamaño de la muestra es grande y el recorrido de la variable es pequeño, por lo que hay valores de la variable que se repiten.
Por ejemplo, si preguntamos el número de personas activas que hay en 50 familias obtenemos la siguiente tabla:
Personas Activas en 50 familias
| 2 | 1 | 2 | 2 | 1 | 2 | 4 | 2 | 1 | 1 |
| 2 | 3 | 2 | 1 | 1 | 1 | 3 | 4 | 2 | 2 |
| 2 | 2 | 1 | 2 | 1 | 1 | 1 | 3 | 2 | 2 |
| 3 | 2 | 3 | 1 | 2 | 4 | 2 | 1 | 4 | 1 |
| 1 | 3 | 4 | 3 | 2 | 2 | 2 | 1 | 3 | 3 |
Podemos observar que la variable toma valores comprendidos entre 1 y 4, por lo que precisaremos una tabla en la que resumamos estos datos quedando la siguiente tabla:
| Personas activas | Número de familias |
| 1 | 16 |
| 2 | 20 |
| 3 | 9 |
| 4 | 5 |
| total | 50 |
Tablas Tipo III
Cuando el tamaño de la muestra y el recorrido de la variable son grandes, por lo que será necesario agrupar en intervalos los valores de la variable. Tambien obligatorio usarla cuando la variable sea cuantitativa continua.
Por ejemplo si a un grupo de 30 alumnos les preguntamos el dinero que en ese momento tienen ahorrado, nos encontramos con los siguientes datos:
| 450 | 1152 | 250 | 300 | 175 | 80 | 25 | 2680 | 605 | 785 |
| 1595 | 2300 | 5000 | 1200 | 100 | 5 | 180 | 200 | 675 | 500 |
| 375 | 1500 | 205 | 985 | 185 | 125 | 315 | 425 | 560 | 1100 |
La variable estadística tiene un recorrido muy grande, (Mayor valor - Menor valor = 5000 - 5 = 4995), por lo que sí queremos hacer una tabla con estos datos tendremos que tomar intervalos. Para decidir la amplitud de los intervalos, necesitaremos decidir ¿cuántos intervalos queremos?. Normalmente se suele trabajar con no más de 10 o 12 intervalos.
|
|
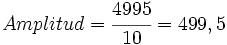
Por lo que tomaremos intervalos de amplitud 500
Debemos tener en cuenta las siguientes consideraciones:
Tomar pocos intervalos implica que la "pérdida de información" sea mayor.
Los intervalos serán siempre Cerrados por la izquierda y Abiertos por la Derecha [Li-1 , Li).
Con estas recomendaciones tendremos la siguiente tabla:
| Intervalo | Nº alumnos |
| [0,500) | 16 |
| [500,1000) | 6 |
| [1000,1500) | 3 |
| [1500,2000) | 2 |
| [2000,2500) | 1 |
| [2500,3000) | 1 |
| [3000,3500) | 0 |
| [3500,4000) | 0 |
| [4000,4500) | 0 |
| [4500,5000) | 0 |
| [5000,5500) | 1 |
Tablas de frecuencias
Ahora iremos añadiendo más columnas según los cálculos y la información que necesitemos. Podemos ir completando la tabla con las frecuencias, que definimos a continuación:
- Frecuencia absoluta. Es el número de veces que aparece cualquier valor de la variable. Se representa por fi. En algunos libros de texto nos la encontraremos representada por ni.
- Frecuencia absoluta acumulada. Es la suma de la frecuencia absoluta de un valor de la variable con todos los anteriores. Se representa por Fi.
- Frecuencia relativa. Es el cociente entre la frecuencia absoluta y el número de datos (N). Se representa por hi. En algunos libros de texto nos la encontraremos representada por ri. Al multiplicarla por 100 obtenemos el porcentaje de individuos que presentan esta característica.
- Frecuencia relativa acumulada. Es la suma de la frecuencia relativa de un valor de la variable con todos los anteriores. También se puede definir como el cociente entre la frecuencia absoluta acumulada y el número total de datos. Se representa por Hi.
En las siguientes escenas puedes construir la tabla de frecuencias para variables discretas y continuas.
Actividades
|
Actividad Interactiva: Tablas de frecuencias
1. Variable cuantitativa discreta.
Actividad: Construye en tu cuaderno la tabla para el ejemplo número de hermanos: 2, 3, 2, 3, 3, 3, 3, 4, 2, 2, 2. Una vez que la tienes en tu cuaderno, constrúyela con la escena y compara los resultados.
2. Variable cuantitativa continua.
Actividad: Construye en tu cuaderno la tabla para el ejemplo de la estatura: 1.59, 1.75, 1.71, 1.85, 1.64, 1.62, 1.66, 1.60, 1.63, 1.76, 1.66. Necesitas agrupar los datos en intervalos. Una vez que la tienes en tu cuaderno, constrúyela con la escena y compara los resultados. |
Como puedes observar no se han tenido en cuenta las variables cualitativas. Esto se debe a que al no trabajar con números no se pueden hacer operaciones. Únicamente tendría sentido en la tabla construir las columnas de frecuencias absolutas y relativas, pero no las acumuladas. En el siguiente apartado de gráficos estadísticos también se podrían representar, pero para los apartados de cálculo de parámetros no podremos trabajar con ellas. si tienes interés en alguna representación, sustituye los valores la variable por los números que quieras y represéntalas o construye la tabla
|
Actividades
|
Gráficos
Una vez construida la tabla de frecuencias, vamos a representar mediante distintos gráficos el estudio realizado. Entre los gráficos más utilizado podemos destacar:
Diagrama de barras
Consiste en dos ejes perpendiculares y una barra o rectángulo para cada valor de la variable. Normalmente, se suele colocar en el eje horizontal los valores de la variable (aunque también se puede hacer en el vertical). El otro eje se gradúa según los valores de las frecuencias. La representación gráfica consiste en dibujar una barra o un rectángulo para cada uno de los valores de la variable de altura igual a su frecuencia.
Histograma
Es un caso particular del diagrama anterior en el caso de variables continuas. Si los intervalos son correlativos, los rectángulos aparecen pegados en la representación gráfica. En caso de que la amplitud de los intervalos no se igual para todos, hay que hacer coincidir el área del rectángulo con la frecuencia del intervalo. Un ejemplo muy utilizado de histograma es una pirámide de población.
Polígono de frecuencias
Representamos dos ejes perpendiculares y representamos en el horizontal los valores de la variable y en el vertical las frecuencias. Representamos los puntos que tiene por primera coordenada el valor de la variable y por segunda el valor de la frecuencia. Uniendo todos los puntos obtenemos una línea poligonal que es la representación que buscamos.
Diagrama de sectores
Consiste en dividir un círculo en tantos sectores como valores de la variable. La amplitud de cada sector debe ser proporcional a la frecuencia del valor correspondiente.
Actividades
|
Actividades Interactivas: Gráficos estadísticos
Actividad 1. Diagrama de barras.
Actividad: Representa en tu cuaderno el diagrama de barras para el ejemplo número de hermanos: 2, 3, 2, 3, 3, 3, 3, 4, 2, 2, 2. Una vez que la tienes en tu cuaderno, represéntala con la escena y compara los resultados.
Actividad 2. Histograma.
Actividad: Representa en tu cuaderno el histograma para el ejemplo del número de la estatura: 1.59, 1.75, 1.71, 1.85, 1.64, 1.62, 1.66, 1.60, 1.63, 1.76, 1.66, según hayas agrupados los datos en intervalos.Una vez que lo tienes en tu cuaderno, represéntalo con la escena y compara los resultados.
Actividad 3. Polígono de frecuencias.
Actividad: Representa en tu cuaderno el polígono de frecuencias para el ejemplo del número de hermanos: 2, 3, 2, 3, 3, 3, 3, 4, 2, 2, 2.Una vez que lo tienes en tu cuaderno, represéntalo con la escena y compara los resultados.
Actividad 4. Diagrama de sectores.
Actividad: Representa en tu cuaderno el polígono de frecuencias para el ejemplo del número de hermanos: 2, 3, 2, 3, 3, 3, 3, 4, 2, 2, 2.Una vez que lo tienes en tu cuaderno, represéntalo con la escena y compara los resultados. |
|
Actividad Actividad 1:
|
Parámetros Estadísticos
Después de haber representado los datos gráficamente, ahora llega el momento de hacer un estudio de los mismos. Si estamos estudiando la estatura de todos los alumnos y alumnas del instituto y necesitamos dar información de este estudio, parece lógico dar un dato que conocemos todos como media y que representa la estatura de todo el alumnado estudiado. Además de este dato existen otros datos (que llamaremos parámetros) que van a representar a toda la población o que nos van a informar sobre la población.
Parámetros estadísticos: Son datos que resumen el estudio realizado en la población. Pueden ser de dos tipos:
- Parámetros de centralización. Son datos que representan de forma global a toda la población. Entre ellos vamos a estudiar la media aritmética, la moda y la mediana.
- Parámetros de dispersión. Son datos que informan de la concentración o dispersión de los datos respecto de los parámetros de centralización. Por ejemplo el recorrido, la varianza y la desviación típica.
Parámetros de centralización
Media aritmética
Se define la media aritmética como la suma de todos los datos dividida por el número de datos. Se representa por 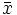 .
.
Para calcular la media aritmética hacemos:
|
|
donde 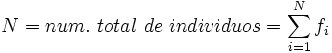 .
.
Sin embargo, podemos observar que aparecen datos repetidos y que en un estudio estadístico tenemos los datos agrupados en una tabla en la que aparecen las frecuencias. Por tanto, podemos simplificar el cálculo de la media aritmética con la fórmula:
|
|
Si la variable es continua, el cálculo se hace de la misma forma pero utilizando como xi las marcas de clase: los valores centrales de cada intervalo o la media aritmética de los extremos de cada intervalo.
|
Actividad Interactiva: Media aritmética
Actividad 1. Variable discreta.
Actividad: Calcula en tu cuaderno la media para el ejemplo número de hermanos: 2, 3, 2, 3, 3, 3, 3, 4, 2, 2, 2. Una vez que la tienes en tu cuaderno, calcúlala con la escena y compara los resultados.
Actividad 2. Variable continua.
Actividad: Calcula en tu cuaderno el histograma para el ejemplo del número de la estatura: 1.59, 1.75, 1.71, 1.85, 1.64, 1.62, 1.66, 1.60, 1.63, 1.76, 1.66, según hayas agrupados los datos en intervalos. Una vez que lo tienes en tu cuaderno, calcúlala con la escena y compara los resultados. |
|
Actividades: Media Aritmética Actividad 1:
Actividad 2:
|
Moda
Se define la moda como el valor de la variable que más se repite, es el decir, aquél que tiene mayor frecuencia absoluta. Se representa por Mo.
Vamos a distinguir para el cálculo de la moda entre variables discretas y continuas.
Si la variable es discreta, el cálculo de la moda no presenta ninguna dificultad, únicamente observamos las frecuencias, vemos cuál es la mayor y la moda será el valor de la variable correspondiente a dicha frecuencia.
Sin embargo si la variable es continua la mayor frecuencia absoluta corresponde a un intervalo, del que decimos que es el intervalo modal. Pero si queremos calcular un único valor de la variable para la moda, aplicamos la siguiente fórmula:
|
|
fMo − 1 y fMo + 1 son las frecuencias del intervalo modal, el anterior y el posterior.
|
Actividad Interactiva: Moda
Actividad 1. Variable discreta.
Actividad: Calcula en tu cuaderno la moda para el ejemplo número de hermanos: 2, 3, 2, 3, 3, 3, 3, 4, 2, 2, 2. Una vez que la tienes en tu cuaderno, calcúlala con la escena y compara los resultados.
Actividad 2. Variable continua.
Actividad: Calcula en tu cuaderno la moda para el ejemplo de la estatura: 1.59, 1.75, 1.71, 1.85, 1.64, 1.62, 1.66, 1.60, 1.63, 1.76, 1.66, utilizando los mismos intervalos que hayas construido antes. Una vez que la tienes en tu cuaderno, calcúlala con la escena y compara los resultados. |
|
Actividad: Moda Actividad 1:
Actividad 2: En este caso de la estatura, se ha calculado la moda utilizando intervalos, pero como tenemos pocos valores de la variable, si los observamos, ¿cuál es la moda? ¿Coincide el resultado? ¿Por qué ? |
Mediana
Si ordenamos todos los valores de la variable de menor a mayor, se define la mediana como el valor de la variable que está en el centro. Se representa por Me. Aquí tenemos que comprender que si hay un número impar de valores, habrá un sólo valor central; mientras que si hay un número par de valores habrá dos valores centrales. Si la variable es discreta y el número de datos es par, la mediana será la media aritmética de los dos valores centrales.
Si la variable es continua, no distinguiremos si el número de datos es par o impar, tendremos un intervalo para la mediana. Igual que se ha hecho con la moda podemos suponer que los datos se distribuyen uniformemente en los intervalos y calcular la mediana con la siguiente fórmula:
|
|
|
Actividad Interactiva: Mediana
Actividad 1. Variable discreta.
Actividad: Calcula en tu cuaderno la mediana para el ejemplo número de hermanos: 2, 3, 2, 3, 3, 3, 3, 4, 2, 2, 2. Una vez que la tienes en tu cuaderno, calcúlala con la escena y compara los resultados.
Actividad 2. Variable continua.
Actividad: Calcula en tu cuaderno la mediana para el ejemplo de la estatura: 1.59, 1.75, 1.71, 1.85, 1.64, 1.62, 1.66, 1.60, 1.63, 1.76, 1.66, utilizando los mismos intervalos que hayas construido antes.Una vez que la tienes en tu cuaderno, calcúlala con la escena y compara los resultados. |
|
Actividad: Mediana Actividad 1:
Actividad 2: En este caso de la estatura, se ha calculado la mediana utilizando intervalos, pero como tenemos pocos valores de la variable, ordénalos de menor a mayor y calcula el resultado, ¿cuál es la mediana? ¿Coincide el resultado? ¿Por qué ? |
Parámetros de dispersión
Recorrido
Se define el recorrido como la diferencia entre el mayor y el menor de los valores de la variable. Se representa por R. Nos indica un intervalo en el que están comprendido todos los datos.
Varianza y desviación típica
Se define la varianza como la media aritmética de los cuadrados de las desviaciones respecto de la media. Es decir:
|
|
Se calcula más facilmente, con la siguiente fórmula equivalente:
|
|
Si la variable es continua, el cálculo se hace de la misma forma pero utilizando como xi las marcas de clase: los valores centrales de cada intervalo o la media aritmética de los extremos de cada intervalo.
|
Actividad Interactiva: Varianza y desviación típica
Actividad 1. Variable discreta.
Actividad: Calcula en tu cuaderno la varianza y desviación típica para el ejemplo número de hermanos: 2, 3, 2, 3, 3, 3, 3, 4, 2, 2, 2. Una vez que la tienes en tu cuaderno, calcúlala con la escena y compara los resultados.
Actividad 2. Variable continua.
Actividad: Calcula en tu cuaderno el la varianza y desviación típica para el ejemplo del número de la estatura: 1.59, 1.75, 1.71, 1.85, 1.64, 1.62, 1.66, 1.60, 1.63, 1.76, 1.66, según hayas agrupados los datos en intervalos. Una vez que lo tienes en tu cuaderno, calcúlala con la escena y compara los resultados. |
|
Actividades Actividad 1:
Actividad 2:
|
Interpretación conjunta de la media y la desviación típica
De todas los parámetros estudiados, los más significativos son la media para las medidas de centralización y la desviación típica para las medidas de dispersión.
Vamos a hacer un estudio conjunto de ambas para entender mejor su significado.
La media aritmética es el centro de gravedad de la distribución estadística. Si nos imaginamos el diagrama de barras o el histograma de frecuencias apoyado en un punto del eje horizontal de forma que quedase en equilibrio, el valor de este punto en dicho eje sería el valor de la media.
Como ya hemos comentado, no es suficiente con un parámetro de centralización, es necesario un parámetro de dispersión que nos indique si los datos estudiados están más concentrados o más dispersos. Y este parámetro de dispersión va a ser la desviación típica. Lógicamente si los datos están más concentrados la desviación típica será menor, y si los datos están más dispersos la desviación típica será mayor.
|
Actividad Interactiva: Interpretación conjunta de la media y la desviación
Actividad 1. Significado de la media y la desviación.
Actividad: Representa, en la escena, el diagrama de barras para el ejemplo del número de hermanos: 2, 3, 2, 3, 3, 3, 3, 4, 2, 2, 2. |
|
Actividades: Significado de la media y la desviación Actividad 1: Modifica los valores de las frecuencias, y si quieres introduce más valores de la variable, hasta que el número de datos sea, por ejemplo, N=100. Construye ejemplos con las siguientes características: a) Dale a todas las frecuencias el mismo valor (el que quieras). ¿Cuánto vale la media? ¿Es lógico este resultado? ¿Cuánto vale la desviación típica? b) Ve disminuyendo en varios pasos las frecuencias de los valores centrales y aumentando por igual las frecuencias de los valores extremos, sin que varíe la media ni el número de datos. ¿Qué ocurre con la desviación típica? ¿Por qué sucede esto? c) Realiza ahora el procedimiento inverso, ve aumentando en varios pasos las frecuencias de los valores centrales y disminuyendo por igual las frecuencias de los valores extremos, sin que varíe la media ni el número de datos. ¿Qué ocurre con la desviación típica? ¿Por qué sucede esto? d) ¿Cómo será una variable estadística con desviación típica igual a 0? ¿Compruébalo en la escena? |
Coeficiente de variación. Si hemos realizado un estudio estadístico en dos poblaciones diferentes, y queremos comparar resultados, no podemos acudir a la desviación típica para ver la mayor o menor homogeneidad de los datos, sino a otro parámetro nuevo, llamado coeficiente de variación y que se define como el cociente entre la desviación típica y la media.
|
|
Por ejemplo, en una exposición de ganado estudiamos un conjunto de vacas con una media de 500 kilos y una desviación típica de 50 kilos. Y observamos también un conjunto de perros con una media de 40 kilos y una desviación típica de 10 kilos. ¿Qué grupo de animales es más homogéneo?
Un razonamiento falso sería decir que el conjunto de perros es más homogéneo porque su desviación típica es más pequeña, pero si calculamos el coeficiente de variación para ambos:
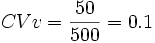 ;
; 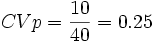
Por tanto, es más homogéneo el conjunto de las vacas.
Parámetros de posición
- Cuartiles. Son valores que dividen a la población en cuatro partes iguales. Los vamos a representar por C1,C2y C3. Entre cada dos de ellos estará el 25 % de los datos. Lógicamente el segundo cuartil coincidirá con la mediana.
- Deciles. Son valores que dividen a la población en diez partes iguales. Los representaremos por Dn. El quinto decil coincide también con la mediana.
- Percentiles. Son valores que dividen a la población en cien partes iguales. Los representamos por Pn. Evidentemente los percentiles 25, 50 y 75 coinciden con los cuartiles. Y los percentiles 10, 20 , ... , 90 coinciden con los deciles.
El cálculo de estos parámetros, tanto para variables discretas como para variables continuas, se hace de forma similar al cálculo de la mediana.
Si la variable es discreta, para calcular un percentil, calcularemos el porcentaje de datos que corresponde a dicho percentil, es decir para calcular el percentil de orden "p", calcularemos 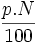 . Si este valor no coincide con ninguna de las frecuencias absolutas acumuladas, cogemos el primer valor de la variable cuya frecuencia absoluta acumulada supera este dato. Pero si este valor coincide con una frecuencia absoluta acumulada, el percentil buscado será la media aritmética entre el valor de la variable correspondiente y el siguiente.
. Si este valor no coincide con ninguna de las frecuencias absolutas acumuladas, cogemos el primer valor de la variable cuya frecuencia absoluta acumulada supera este dato. Pero si este valor coincide con una frecuencia absoluta acumulada, el percentil buscado será la media aritmética entre el valor de la variable correspondiente y el siguiente.
Si la variable es continua aplicamos la siguiente fórmula muy similar a la utilizada para el cálculo de la mediana:
|
|
|
Actividad Interactiva: Percentiles
Actividad 1. Variable discreta.
Actividad: Calcula en tu cuaderno los cuartiles primero y tercero para el ejemplo del número de hermanos: 2, 3, 2, 3, 3, 3, 3, 4, 2, 2, 2.Una vez que los tienes en tu cuaderno, calcúlalos con la escena y compara los resultados.
Actividad 2. Variable continua.
Actividad: Calcula en tu cuaderno los cuartiles primero y tercero para el ejemplo de la estatura: 1.59, 1.75, 1.71, 1.85, 1.64, 1.62, 1.66, 1.60, 1.63, 1.76, 1.66, utilizando los mismos intervalos que hayas construido antes. Una vez que los tienes en tu cuaderno, calcúlalos con la escena y compara los resultados. |
|
Actividad: Percentiles Actividad 1: Modifica las frecuencias y calcula varios percentiles. |
Medidas de forma
Coeficiente de asimetría de Fisher
Permite interpretar la forma de la distribución, respecto a ser o no simétrica.
|
|
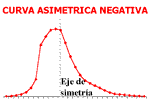
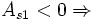 distribución asimétrica negativa; existe mayor concentración de valores a la izquierda de la media que a su derecha).
distribución asimétrica negativa; existe mayor concentración de valores a la izquierda de la media que a su derecha).
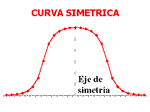
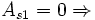 distribución simétrica; existe la misma concentración de valores a la derecha y a la izquierda de la media).
distribución simétrica; existe la misma concentración de valores a la derecha y a la izquierda de la media).
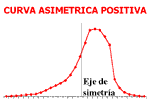
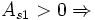 distribución asimétrica positiva; existe mayor concentración de valores a la derecha de la media que a su izquierda)
distribución asimétrica positiva; existe mayor concentración de valores a la derecha de la media que a su izquierda)
Coeficiente de curtosis
Recibe también el nombre de coeficiente de concentración central, midiendo el grado de aplastamiento o apuntamiento de la gráfica de la distribución de la variable estadística. Una mayor concentración de datos en torno al promedio harán que la forma sea alargada, siendo tanto más plana (o aplastada) cuanto mayor sea la dispersión de los mismos.
|
|
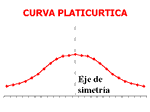
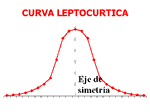
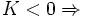 Distribución platicúrtica: presenta un reducido grado de concentración alrededor de los valores centrales de la variable.
Distribución platicúrtica: presenta un reducido grado de concentración alrededor de los valores centrales de la variable.
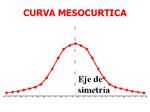
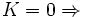 Distribución mesocúrtica: presenta un grado de concentración medio alrededor de los valores centrales de la variable (el mismo que presenta una distribución normal).
Distribución mesocúrtica: presenta un grado de concentración medio alrededor de los valores centrales de la variable (el mismo que presenta una distribución normal).
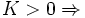 Distribución leptocúrtica: presenta un elevado grado de concentración alrededor de los valores centrales de la variable.
Distribución leptocúrtica: presenta un elevado grado de concentración alrededor de los valores centrales de la variable.
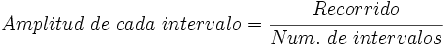
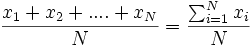
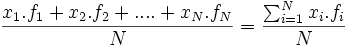
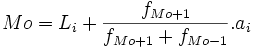
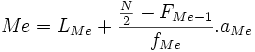
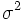 =
=