Plantilla:Dominio e imagen de una función
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 09:35 3 nov 2016 Coordinador (Discusión | contribuciones) (→Dominio e imagen de una función) ← Ir a diferencia anterior |
Revisión de 10:00 3 nov 2016 Coordinador (Discusión | contribuciones) (→Razones para restringir el dominio de una función) Ir a siguiente diferencia → |
||
| Línea 29: | Línea 29: | ||
| :d) Su dominio es <math>(0, + \infty)</math>, porque el lado de un cuadrado sólo puede tomar valores positivos | :d) Su dominio es <math>(0, + \infty)</math>, porque el lado de un cuadrado sólo puede tomar valores positivos | ||
| }} | }} | ||
| - | {{p}} | ||
| - | |||
| {{p}} | {{p}} | ||
| {{ejercicio | {{ejercicio | ||
| Línea 43: | Línea 41: | ||
| {{p}} | {{p}} | ||
| |sol= | |sol= | ||
| - | a) Es función. <math>D=[-3.5, 4]\;\!</math>. <math>Im=[-4, 3]\;\!</math>. | + | a) Es función. <math>Dom=[-3.5, 4]\;\!</math>. <math>Im=[-4, 3]\;\!</math>. |
| b) No es función.<br> | b) No es función.<br> | ||
| c) No es función.<br> | c) No es función.<br> | ||
Revisión de 10:00 3 nov 2016
Dominio e imagen de una función
- El conjunto de valores de la variable independiente,
, para los que hay un valor de la variable dependiente, 
, se llama dominio de definición de la función. Se denota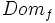 
.
- El conjunto de valores que toma la variable independiente, , se llama imagen, recorrido o rango de la función. Se denota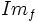
.
- Si un punto (x,y) pertenece a la gráfica de la función entonces se dice que y es la imagen de x y también que x es la antiimagen de y.
![Dom_f=[0,100]\;](/wikipedia/images/math/a/b/d/abd624243bc89fe5a2233724f02b4f4a.png)
![Im_f=[0,200]\;](/wikipedia/images/math/3/9/f/39fa0225481adedcbe46a7b134738d1a.png)
Razones para restringir el dominio de una función
- Imposibilidad de realizar alguna operación con ciertos valores de (Por ejemplo: denominadores que se anulan, radicandos que toman valores negativos,...)
- Contexto en el que se estudia la función (Por ejemplo, una función que relaciona lado y área de una figura plana, no puede tomar valores negativos)
- Por voluntad de quien propone la función.
Ejemplo: Dominio de definición de una función
- Halla el dominio de las funciones:
- a)
![y=x-3 \ , \quad x \in [-1,1]\;\!](/wikipedia/images/math/b/2/f/b2f9332046e953e44d840dc3a97e95ea.png)
- a)
- b)
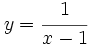
- b)
- c)
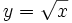
- c)
- d)
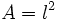(Área de un cuadrado de lado 
)
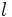- d)
Solución:[Mostrar]
![[-1,1]\;\!](/wikipedia/images/math/d/e/f/defe3e8e42c39a844e648621afe1619e.png)
, por voluntad del que ha definido la función, ya que, en principio, cualquier valor de 
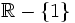, porque el denominador no puede tomar el valor cero, ya que imposibilitaría hacer la división.
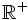, porque el radicando no puede ser negativo para poder hallar la raíz.
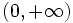, porque el lado de un cuadrado sólo puede tomar valores positivos Ejercicios: Dominio e imagen 1. Indica cuál de las gráficas siguientes representan una función. En caso de ser función, indica su dominio y su imagen. Solución:[Mostrar]
|
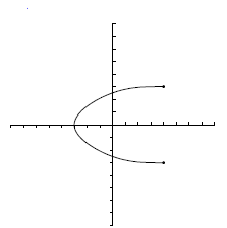
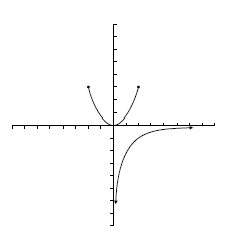
![Dom=[-3.5, 4]\;\!](/wikipedia/images/math/c/b/4/cb4d06ad9717b5428bfec1aa7001daab.png)
. ![Im=[-4, 3]\;\!](/wikipedia/images/math/4/9/c/49cf9064f7a20c06eb8cb9c71af85beb.png)
.
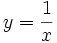 Actividad: Dominio e imagen de una función
|
.
