Plantilla:Continuidad de funciones
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 10:19 5 nov 2016 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 10:24 5 nov 2016 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 28: | Línea 28: | ||
| :a) <math>y=x^3+x\;</math> no presenta discontinuidades. | :a) <math>y=x^3+x\;</math> no presenta discontinuidades. | ||
| :b) <math>y=\frac{1}{x}</math> presenta una discontinuidad en x=0. | :b) <math>y=\frac{1}{x}</math> presenta una discontinuidad en x=0. | ||
| + | :b) <math>y=\frac{1}{x}\, , \ x \in [1,10]</math> no presenta discontinuidades en ese intervalo. | ||
| - | {{p}} | ||
| - | |sol= | ||
| - | Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones: | ||
| - | |||
| - | :a) Obtén el dominio y la imagen de la función <math>y=x^3+x</math>. | ||
| - | :b) Obtén el dominio y la imagen de la función <math>y=\frac{1}{x}</math>. | ||
| - | |||
| - | {{p}} | ||
| |sol= | |sol= | ||
| Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones: | Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones: | ||
| :a) {{consulta|texto=plot x^3+x}} | :a) {{consulta|texto=plot x^3+x}} | ||
| - | :b) {{consulta|texto= plot 1/x, x from -10 to 10}} | + | :b) {{consulta|texto= plot 1/x}} |
| + | :c) {{consulta|texto= plot 1/x, x from 1 to 10}} | ||
| {{widget generico}} | {{widget generico}} | ||
Revisión de 10:24 5 nov 2016
- Cuando la gráfica de una función tiene saltos bruscos (no se puede dibujar de un solo trazo) decimos que es discontinua. En caso contrario se dice que es continua. Los puntos donde se producen los saltos se llaman discontinuidades.
- Una función diremos que es continua en un intervalo si no presenta ninguna discontinuidad en dicho intervalo, aunque pueda presentar alguna fuera del mismo.
Ejemplos: Continuidad
De las siguientes funciones, indica cuáles son continuas y cuáles no. Enumera las discontinuidades.
Solución:
Solución:
Las funciones a) y c) son continuas.
La b) es discontinua con discontinuidades en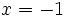 y
y  .
.|
Actividad: Continuidad de funciones Observa las gráficas de las siguientes funciones y si tienen o no discontinuidades:
|
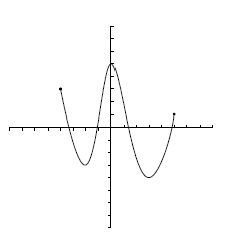
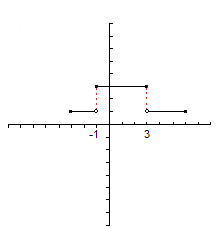
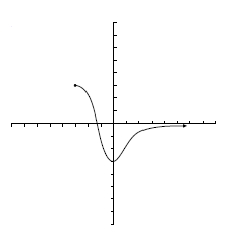
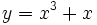 no presenta discontinuidades.
no presenta discontinuidades.
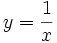 presenta una discontinuidad en x=0.
presenta una discontinuidad en x=0.
![y=\frac{1}{x}\, , \ x \in [1,10]](/wikipedia/images/math/b/d/6/bd68b28d4862afc025e586193eac9bf1.png) no presenta discontinuidades en ese intervalo.
no presenta discontinuidades en ese intervalo.
