Plantilla:Máximos y mínimos de una función
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 09:47 6 nov 2016 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 09:50 6 nov 2016 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 8: | Línea 8: | ||
| {{Geogebra_enlace | {{Geogebra_enlace | ||
| |descripcion=En esta escena podrás ver cuando una función alcanza un máximo o un mínimo. | |descripcion=En esta escena podrás ver cuando una función alcanza un máximo o un mínimo. | ||
| - | |enlace=[https://ggbm.at/yJZpJ93k Actividad 1: Crecimiento. Máximos y mínimos] | + | |enlace=[https://ggbm.at/yJZpJ93k Actividad 1: Extremos de una función] |
| }} | }} | ||
| {{p}} | {{p}} | ||
| {{Geogebra_enlace | {{Geogebra_enlace | ||
| |descripcion=Interpreta la siguiente gráfica que muestra las temperaturas a lo largo de un día de invierno en un pueblo de Valladolid. | |descripcion=Interpreta la siguiente gráfica que muestra las temperaturas a lo largo de un día de invierno en un pueblo de Valladolid. | ||
| - | |enlace=[https://ggbm.at/JGfZ3v4T Actividad 2: Crecimiento. Máximos y mínimos] | + | |enlace=[https://ggbm.at/JGfZ3v4T Actividad 2: Extremos de una función] |
| }} | }} | ||
| {{p}} | {{p}} | ||
Revisión de 09:50 6 nov 2016
- Una función
 tiene un máximo relativo en un punto
tiene un máximo relativo en un punto 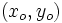 cuando
cuando 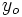 es mayor que los valores que toma la variable
es mayor que los valores que toma la variable  en un intervalo entorno al punto.
en un intervalo entorno al punto.
- Una función
 tiene un mínimo relativo en un punto
tiene un mínimo relativo en un punto 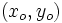 cuando
cuando 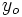 es menor que los valores que toma la variable
es menor que los valores que toma la variable  en un intervalo entorno al punto.
en un intervalo entorno al punto.
En esta escena podrás ver cuando una función alcanza un máximo o un mínimo.
Interpreta la siguiente gráfica que muestra las temperaturas a lo largo de un día de invierno en un pueblo de Valladolid.
|
Actividad: Crecimiento. Máximos y mínimos
Construye una grafica que cumpla ciertas condiciones de crecimiento, de máximos y mínimos.
Actividad: En la siguiente escena se representa la gráfica de una función creciente en el intervalo [0,8], decreciente en el intervalo [8,16] y creciente de nuevo en el intervalo [16,24]. La función alcanza un máximo en el punto B y un mínimo en el punto C. Arrastra los puntos A, B, C y D para representar gráficas con las siguientes características. En cada caso, escribe en tu cuaderno en qué intervalos la función es creciente y en cuáles es decreciente: a) Pasa por los puntos (0,3) y (24,0), alcanza un máximo en el punto (8,6), un mínimo en el punto (16,-5). b) Pasa por el punto (0,5) y se mantiene constante en todo el intervalo [0, 8], alcanza un mínimo en (16, -1) y un máximo en (24,8). |

