Plantilla:Cálculo de la pendiente

(Diferencia entre revisiones)

Revisión de 19:13 9 nov 2016

Proposición

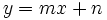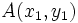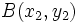Consideremos una función afín $y=mx+n\;$ y dos puntos $A(x_1,y_1)\;$ y $B(x_2,y_2)\;$ de la recta que la representa.

La pendiente se puede calcular de la siguiente manera:

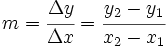
$m=\cfrac {\Delta y}{\Delta x}=\cfrac {y_2-y_1}{x_2-x_1}$

Demostración:

Como 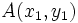$A(x_1,y_1)\;$ es un punto de la recta, verifica su ecuación: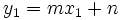 $y_1=mx_1+n\;$

Como 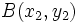$B(x_2,y_2)\;$ es otro punto de la recta, también verifica su ecuación: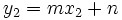 $y_2=mx_2+n\;$

Restando ambas expresiones:

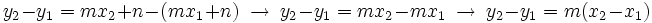
$y_2-y_1=mx_2+n-(mx_1+n) \ \rightarrow \ y_2-y_1=mx_2-mx_1 \ \rightarrow \ y_2-y_1=m(x_2-x_1)$

y despejando m:

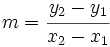
$m=\cfrac{y_2-y_1}{x_2-x_1}$

Cálculo de la pendiente a partir de dos puntos Descripción:

Escena en la que aprenderás a calcular la pendiente de una función lineal.

Autoevaluación: Cálculo de la pendiente a partir de dos puntos Descripción:

Practica el cálculo de la pendiente de una función lineal a partir de dos puntos.

 {{Teorema|titulo=Proposición|enunciado=Consideremos una función afín <math>y=mx+n\;</math> y dos puntos <math>A(x_1,y_1)\;</math> y <math>B(x_2,y_2)\;</math> de la recta que la representa.
 {{p}}
 {{Geogebra_enlace
-|descripcion=Escena en la que aprenderás a calcular la pendiente de una función afín.
+|descripcion=Escena en la que aprenderás a calcular la pendiente de una función lineal.
 |enlace=[https://ggbm.at/QMSK9432 Cálculo de la pendiente a partir de dos puntos]
 }}
 {{p}}
 {{Geogebra_enlace
-|descripcion=Practica el cálculo de la pendiente de una función afín a partir de dos puntos.
+|descripcion=Practica el cálculo de la pendiente de una función lineal a partir de dos puntos.
 |enlace=[https://ggbm.at/jSMNQrbM Autoevaluación: Cálculo de la pendiente a partir de dos puntos]
 }}