Plantilla:Area elipse
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 18:44 17 nov 2016 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión actual Coordinador (Discusión | contribuciones) |
||
| Línea 1: | Línea 1: | ||
| {{Caja_Amarilla|texto= | {{Caja_Amarilla|texto= | ||
| {{Tabla3 | {{Tabla3 | ||
| - | |celda1= | + | |celda1={{b}} |
| - | [[Imagen:elipse_a_b.png|160px]] | + | {{p}} |
| + | [[Imagen:elipse_a_b.png|220px]] | ||
| |celda2={{p}} | |celda2={{p}} | ||
| * '''Perímetro:''' | * '''Perímetro:''' | ||
| Línea 14: | Línea 15: | ||
| :<math>b\;</math>: semieje menor. | :<math>b\;</math>: semieje menor. | ||
| - | * '''Nota:''' | + | * '''Notas:''' |
| :<math>\pi\;\!</math>: número Pi = 3,14159...{{p}} | :<math>\pi\;\!</math>: número Pi = 3,14159...{{p}} | ||
| :La fórmula del perímetro es una aproximación obtenida por [[Ramanujan]]. Una fórmula exacta requiere del uso de series. | :La fórmula del perímetro es una aproximación obtenida por [[Ramanujan]]. Una fórmula exacta requiere del uso de series. | ||
| }} | }} | ||
| - | }} {{p}} | ||
| - | {{Desplegable|titulo=Demostración:{{b}}|contenido= | ||
| - | La fórmula del área del sector circular se obtiene a partir de la del área del círculo, aplicando una regla de tres. | ||
| - | |||
| - | |||
| - | <center><math>\begin{matrix}A_{Sect} & \to & \alpha \\ A_{Circ} & \to & 360^o \end{matrix}</math></center> | ||
| - | |||
| - | Despejando el área del sector: | ||
| - | |||
| - | <center><math>A_{Sect}=\cfrac{A_{Circ} \cdot \alpha}{360^o}</math></center> | ||
| - | |||
| - | |||
| - | de donde, sustituyendo el área del círculo por su valor, <math>\pi r^2\;\!</math>, se obtiene la fórmula. | ||
| - | |||
| - | |||
| - | Lo mismo ocurre con la de la longitud del arco, que se obtiene a partir de la de la longitud de la circunferencia, también mediante una regla de tres. | ||
| - | |||
| - | |||
| - | <center><math>\begin{matrix}L_{Sect} & \to & \alpha \\ L_{Circ} & \to & 360^o \end{matrix}</math></center> | ||
| - | |||
| - | Despejando la longitud del sector: | ||
| - | |||
| - | <center><math>L_{Sect}=\cfrac{L_{Circ} \cdot \alpha}{360^o}</math></center> | ||
| - | |||
| - | |||
| - | de donde, sustituyendo la longitud de la circunferencia por su valor, <math>2 \pi r\;\!</math>, se obtiene la fórmula. | ||
| - | ---- | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| {{Geogebra_enlace | {{Geogebra_enlace | ||
| - | |descripcion=En esta escena podrás hallar el área del sector circular y la longitud del arco de circunferencia correspondiente. | + | |descripcion=En esta escena podrás hallar el área y el perímetro aproximado de la elipse. |
| - | |enlace=[https://ggbm.at/g94ejTfk Área del sector circular y longitud de su arco] | + | |enlace=[https://www.geogebra.org/m/wekZJJG4 Área y perímetro de la elipse] |
| }} | }} | ||
| {{p}} | {{p}} | ||
| - | {{wolfram desplegable|titulo=El sector circular|contenido= | + | {{wolfram desplegable|titulo=La elipse|contenido= |
| {{wolfram | {{wolfram | ||
| - | |titulo=Actividad: ''El sector circular'' | + | |titulo=Actividad: ''La elipse'' |
| |cuerpo= | |cuerpo= | ||
| {{ejercicio_cuerpo | {{ejercicio_cuerpo | ||
| |enunciado= | |enunciado= | ||
| - | :a) Halla el área de un sector circular de radios 3 m y ángulo central 45º. | + | Halla el área de una elipse cuyos semiejes miden 3 y 5 cm, respectivamente. |
| - | :b) Halla el perímetro de un sector circular de radios 3 m y ángulo central 45º. | + | |
| {{p}} | {{p}} | ||
| |sol= | |sol= | ||
| - | Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones: | + | Para averiguar la solución debes escribir donde pone "Escribe tu consulta" la siguiente expresión: |
| - | :a) {{consulta|texto=circular sector, radius 3m, angle 45º, area}} | + | {{consulta|texto=ellipse area, semimajor axis=5 cm, semiminor axis=3 cm}} |
| - | :b) {{consulta|texto=circular sector, radius 3m, angle 45º, perimeter}} | + | |
| {{widget generico}} | {{widget generico}} | ||
Revisión actual
|
|
|
|
![P \approx \pi \left[3(a+b) - \sqrt{(3a+b)(a+3b)}\right]\!\,](/wikipedia/images/math/4/5/3/4531867e543bc27be7c45f80a7599da1.png)
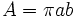
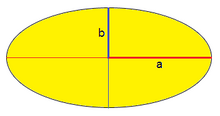
: semieje mayor.
: semieje menor.
: número Pi = 3,14159...
Área y perímetro de la elipse Descripción: En esta escena podrás hallar el área y el perímetro aproximado de la elipse.
Actividad: La elipse Halla el área de una elipse cuyos semiejes miden 3 y 5 cm, respectivamente.
Solución: Para averiguar la solución debes escribir donde pone "Escribe tu consulta" la siguiente expresión: ellipse area, semimajor axis=5 cm, semiminor axis=3 cm |
