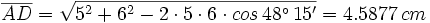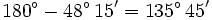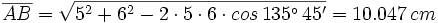Resolución de triángulos cualesquiera (1ºBach)
De Wikipedia
| Revisión de 19:55 19 sep 2016 Coordinador (Discusión | contribuciones) (→Teorema del coseno) ← Ir a diferencia anterior |
Revisión de 00:26 20 nov 2016 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 14: | Línea 14: | ||
| En un triángulo cualquiera se cumplen las siguientes igualdades: | En un triángulo cualquiera se cumplen las siguientes igualdades: | ||
| {{p}} | {{p}} | ||
| - | <center><math>\cfrac{a}{sen \, \hat A}=\cfrac{b}{sen \, \hat B}=\cfrac{c}{sen \, \hat C}</math></center> | + | <center>{{Caja|contenido=<math>\cfrac{a}{sen \, \hat A}=\cfrac{b}{sen \, \hat B}=\cfrac{c}{sen \, \hat C}</math>}}</center> |
| {{p}} | {{p}} | ||
| <br> | <br> | ||
| Línea 98: | Línea 98: | ||
| En un triángulo cualquiera se cumplen la siguiente relación: | En un triángulo cualquiera se cumplen la siguiente relación: | ||
| {{p}} | {{p}} | ||
| - | <center><math>c^2=a^2+b^2-2ab \, cos \, \hat C</math></center> | + | <center>{{Caja|contenido=<math>c^2=a^2+b^2-2ab \, cos \, \hat C</math>}}</center> |
| Analogamente: | Analogamente: | ||
Revisión de 00:26 20 nov 2016
| Enlaces internos | Para repasar o ampliar | Enlaces externos |
| Indice Descartes Manual Casio | T. Coseno | WIRIS Geogebra Calculadoras |
Tabla de contenidos |
(Pág. 116)
Teorema de los senos
Teorema de los senos
|
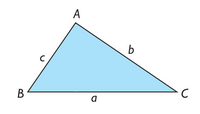
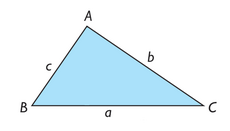
En un triángulo cualquiera se cumplen las siguientes igualdades:
|
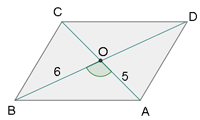
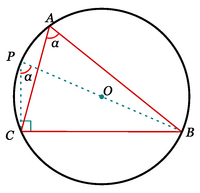
Dado el triángulo ABC, denotamos por O su circuncentro y dibujamos su circunferencia circunscrita. Prolongando el segmento  hasta cortar la circunferencia, se obtiene un diámetro
hasta cortar la circunferencia, se obtiene un diámetro 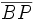 .
.
Ahora, el triángulo PBC es recto, puesto que 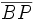 es un diámetro, y además los ángulos
es un diámetro, y además los ángulos 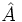 y
y 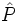 son iguales, porque ambos son ángulos inscritos que abarcan el mismo arco
son iguales, porque ambos son ángulos inscritos que abarcan el mismo arco 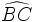 . Por la definición de seno, se tiene
. Por la definición de seno, se tiene
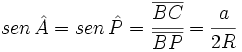
donde R es el radio de la circunferencia. Despejando 2R obtenemos:
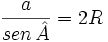
Teorema de los senos con otra demostración.
Ejemplo: Teorema de los senos
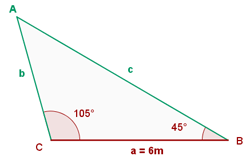
De un triángulo sabemos que: a = 6 m, B = 45° y C = 105°. Calcula los restantes elementos.
Resuelve el triángulo ABC sabiendo que A=35º, B=61º y a=13 cm.
Ejercicios propuestos
|
Ejercicios propuestos: Teorema de los senos |
(Pág. 118)
Teorema del coseno
Teorema del coseno
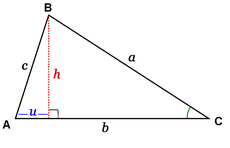
Notemos que el teorema de los cosenos es equivalente al teorema de Pitágoras cuando el ángulo 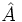 es recto. Por tanto sólo es necesario considerar los casos cuando dicho ángulo es agudo u obtuso.
es recto. Por tanto sólo es necesario considerar los casos cuando dicho ángulo es agudo u obtuso.
Primer caso: 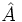 es agudo.
es agudo.
Consideremos la figura adjunta. La altura 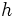 divide al triángulo ABC en dos triángulos rectángulos. El teorema de Pitágoras aplicado a ambos establece que divide al triángulo ABC en dos triángulos rectángulos. El teorema de Pitágoras aplicado a ambos establece que
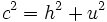 y y 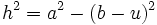 Combinando ambas ecuaciones y luego simplificando obtenemos 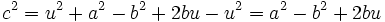 Por la definición de coseno, se tiene: 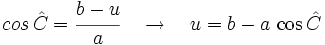 Sustituimos el valor de 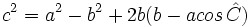 concluyendo que 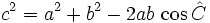 y terminando con esto la prueba del primer caso. |
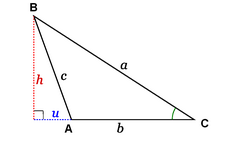
Segundo caso: 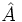 es obtuso.
es obtuso.
Consideremos la figura adjunta. El teorema de Pitágoras establece nuevavamente que
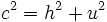 y y 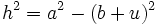 Combinando ambas ecuaciones obtenemos 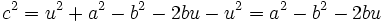 De la definición de coseno, se tiene: 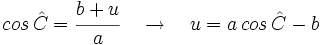 Sustituimos en la expresión para 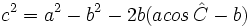 concluyendo nuevamente 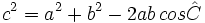 |
Teorema del coseno con demostración.
Ejemplo: Teorema del coseno
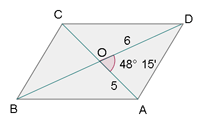
Las diagonales de un paralelogramo miden 10 cm y 12 cm, y el ángulo que forman es de 48° 15'. Calcular los lados.
|
Actividad: Teorema del coseno
Solución: Donde pone "Escribe tu consulta" pon la siguiente expresión:
|
Resuelve el triángulo ABC sabiendo que C=42º, a=13 cm y b=8 cm.
Ejercicios propuestos
|
Ejercicios propuestos: Teorema del coseno |
Videotutoriales
Resolver un triángulo es identificarlo (o sea, determinar sus lados y ángulos); para ello hay que conocer tres de sus elementos, siendo alguno de ellos un lado. Cabe distinguir 4 casos:
- Se conocen dos ángulos y un lado.
- Se conocen dos lados y el ángulo que forman.
- Se conocen dos lados y el ángulo opuesto a uno de ellos.
- Se conocen los tres lados.
Videotutorial.
Videotutorial.
Videotutorial.
Videotutorial.
Videotutorial.
Videotutorial.
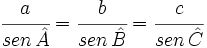
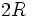 , donde
, donde  es el radio de la circunferencia circunscrita al triángulo.
es el radio de la circunferencia circunscrita al triángulo.
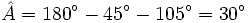
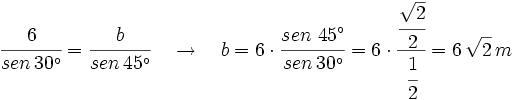
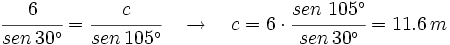
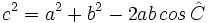

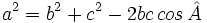
 en la expresión para
en la expresión para 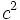 y simplificamos:
y simplificamos: