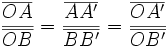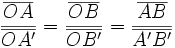Plantilla:Teorema de Tales
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 18:01 21 nov 2016 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 18:01 21 nov 2016 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 24: | Línea 24: | ||
| {{p}} | {{p}} | ||
| <center><math> \frac {\overline{OA}} {\overline{OA'}} = \frac {\overline{OB}} {\overline{OB'}} = \frac {\overline{AB}} {\overline{A'B'}}</math></center> | <center><math> \frac {\overline{OA}} {\overline{OA'}} = \frac {\overline{OB}} {\overline{OB'}} = \frac {\overline{AB}} {\overline{A'B'}}</math></center> | ||
| - | {{}} | + | {{p}} |
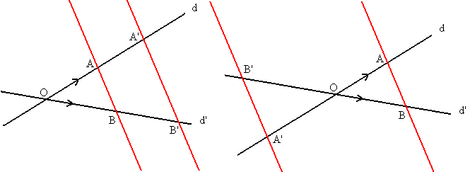
| En consecuencia, los triángulos OAB y OA'B' son semejantes. | En consecuencia, los triángulos OAB y OA'B' son semejantes. | ||
| }} | }} | ||
Revisión de 18:01 21 nov 2016
Primer teorema de Tales
En esta escena podrás comprobar el primer teorema de Tales.