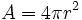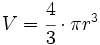Plantilla:Áreas y volúmenes en el espacio
De Wikipedia
| Revisión de 10:22 1 dic 2016 Coordinador (Discusión | contribuciones) (→Cono truncado) ← Ir a diferencia anterior |
Revisión de 11:05 1 dic 2016 Coordinador (Discusión | contribuciones) (→Esfera) Ir a siguiente diferencia → |
||
| Línea 197: | Línea 197: | ||
| {{AI2|titulo=Actividades Interactivas: ''Volumen de la esfera''|cuerpo= | {{AI2|titulo=Actividades Interactivas: ''Volumen de la esfera''|cuerpo= | ||
| {{ai_cuerpo | {{ai_cuerpo | ||
| - | |enunciado='''Actividad 1:''' Halla el volumen de una esfera de 2,1 cm de radio. | + | |enunciado='''Actividad:''' Halla el volumen y la superficie de un balón de futbol. |
| - | |actividad= | + | |
| - | + | ||
| - | Comprueba los resultados en la siguiente escena: | + | |
| - | + | ||
| - | <center><iframe> | + | |
| - | url=http://maralboran.org/web_ma/descartes/1y2_eso/Volumenes_d3/VOLUMENES_6_1.html | + | |
| - | width=530 | + | |
| - | height=390 | + | |
| - | name=myframe | + | |
| - | </iframe></center> | + | |
| - | <center>[http://maralboran.org/web_ma/descartes/1y2_eso/Volumenes_d3/VOLUMENES_6_1.html '''Shift-Click''' aquí si no se ve bien la escena]</center> | + | |
| - | }} | + | |
| - | {{ai_cuerpo | + | |
| - | |enunciado='''Actividad 2:''' ¿Qué relación existe entre el volumen de la esfera y los volúmenes del cilindro y del cono? | + | |
| - | |actividad= | + | |
| - | + | ||
| - | En la siguiente escena modifica los valores del radio y observa los resultados: | + | |
| - | + | ||
| - | <center><iframe> | + | |
| - | url=http://maralboran.org/web_ma/descartes/1y2_eso/Volumenes_d3/VOLUMENES_6_2.html | + | |
| - | width=530 | + | |
| - | height=390 | + | |
| - | name=myframe | + | |
| - | </iframe></center> | + | |
| - | <center>[http://maralboran.org/web_ma/descartes/1y2_eso/Volumenes_d3/VOLUMENES_6_2.html '''Shift-Click''' aquí si no se ve bien la escena]</center> | + | |
| - | + | ||
| - | En consecuencia,si llamamos: | + | |
| - | + | ||
| - | *<math>V_c \;\!</math>= Volumen del cilindro de radio R y altura 2R | + | |
| - | *<math>V_e \;\!</math>= Volumen de la esfera de radio R. | + | |
| - | *<math>V_n \;\!</math>= Volumen del cono de radio R y altura 2R. | + | |
| - | + | ||
| - | entonces: | + | |
| - | + | ||
| - | *<math>V_e=2 \cdot V_n</math> | + | |
| - | *<math>V_c=3 \cdot V_n</math> | + | |
| - | *<math>V_c=V_n+V_e \;\!</math> | + | |
| - | }} | + | |
| - | {{ai_cuerpo | + | |
| - | |enunciado='''Actividad 3:''' Halla el volumen y la superficie de un balón de futbol. | + | |
| |actividad= | |actividad= | ||
| [[Imagen:balon.jpg |left]] | [[Imagen:balon.jpg |left]] | ||
| Línea 260: | Línea 220: | ||
| }} | }} | ||
| + | }} | ||
| + | {{p}} | ||
| + | {{Geogebra_enlace | ||
| + | |descripcion=En esta escena podrás calcular el volumen y área de una esfera. | ||
| + | |enlace=[https://ggbm.at/DRMa7bXj Volúmen y área de la esfera] | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
Revisión de 11:05 1 dic 2016
Tabla de contenidos |
Prisma
|
|
En esta escena podrás ver el desarrollo de un prisma recto regular y calcular su volumen y sus áreas.
Ortoedro
Como sabemos, un ortoedro es un prisma recto de base rectangular o cuadrada.
|
|
Cubo
Un caso particular de ortoedro es el cubo cuyas caras son todas cuadradas.
|
|
En esta escena podrás ver el desarrollo de un ortoedro y calcular su volumen y su área.
Pirámide
|
|
En esta escena podrás ver el desarrollo de una pirámide y calcular su volumen y su áreas.
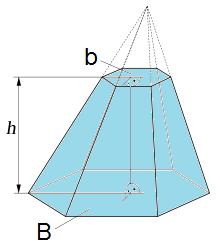
Pirámide truncada
|
|
En esta escena podrás calcular el volumen y las áreas del tronco de pirámide.
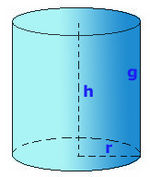
Cilindro
|
|
En esta escena podrás ver el desarrollo de un cilindro y calcular su volumen y sus áreas.
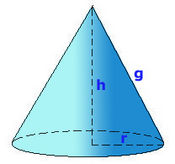
Cono
|
|
En esta escena podrás ver el desarrollo de un cono y calcular su volumen y sus áreas.
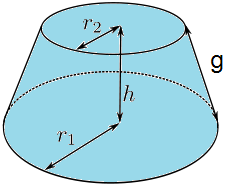
Cono truncado
|
|
En esta escena podrás calcular el volumen y las áreas de un tronco de cono.
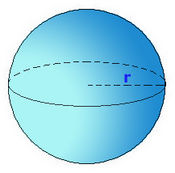
Esfera
|
|
|
Actividades Interactivas: Volumen de la esfera
Actividad: Halla el volumen y la superficie de un balón de futbol.
Actividad: Balón Fútbol Competición, MASTER T-5: Balón técnico para competición. Cubierta de cuero PU Cordley de 32 paneles cosidos. Fabricado bajo norma ISO9002 de acuerdo a las especificaciones FIFA. Sus cuatro capas de poliéster garantizan estabilidad y evitan la deformación del balón. Cámara de látex de doble laminado y válvula de Butyl automática. Datos técnicos:
|
En esta escena podrás calcular el volumen y área de una esfera.
En esta escena podrás comprobar la relación que existe entre los volúmenes de la esfera, el cono y el cilindro.
Ejercicios
|
Actividad Interactiva: Volúmenes de cuerpos irregulares
Actividad 1. Halla el volumen de las siguientes figuras.
Actividad: Halla el volumen de las figuras que aparecen en la siguiente escena. Pulsa las flechas para cambiar la figura.
Actividad 2. Halla el volumen de las siguientes figuras.
Actividad: Halla el volumen de las figuras que aparecen en la siguiente escena. Pulsa las flechas para cambiar la figura. |
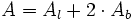
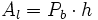
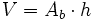
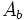 : Área de la base.
: Área de la base.
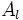 : Área lateral.
: Área lateral.
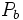 : Perímetro de la base.
: Perímetro de la base.
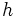 : altura.
: altura.
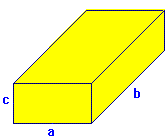
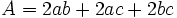
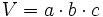
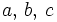 : aristas.
: aristas.
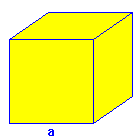
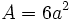
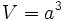
 : arista.
: arista.
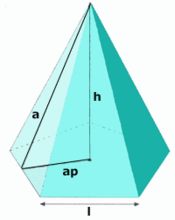
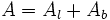
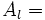 Suma áreas triángulos
Suma áreas triángulos
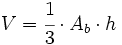
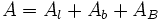
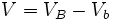
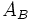 : Área de la base inferior.
: Área de la base inferior.
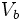 : Volumen de la pirámide pequeña de base b.
: Volumen de la pirámide pequeña de base b.
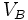 : Volumen de la pirámide completa de base B.
: Volumen de la pirámide completa de base B.
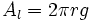
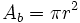
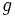 : generatriz.
: generatriz.
 : radio.
: radio.
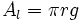
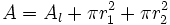
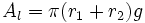
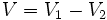
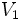 : Volumen del cono completo.
: Volumen del cono completo.
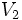 : Volumen del cono pequeño eliminado.
: Volumen del cono pequeño eliminado.