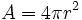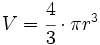Plantilla:Áreas y volúmenes en el espacio
De Wikipedia
| Revisión de 11:28 1 dic 2016 Coordinador (Discusión | contribuciones) (→Esfera) ← Ir a diferencia anterior |
Revisión de 13:32 1 dic 2016 Coordinador (Discusión | contribuciones) (→Prisma) Ir a siguiente diferencia → |
||
| Línea 1: | Línea 1: | ||
| ==Prisma== | ==Prisma== | ||
| - | {{Tabla3 | + | {{Prisma}} |
| - | |celda1= | + | |
| - | <center>[[Imagen:prisma.gif | 175px]]</center> | + | |
| - | |celda2={{p}} | + | |
| - | * '''Áreas:'''{{p}} | + | |
| - | {{Caja|contenido=<math>A=A_l+2 \cdot A_b </math>}}{{p}} | + | |
| - | {{Caja|contenido=<math>A_l=P_b \cdot h </math>}} | + | |
| - | * '''Volumen:'''{{p}} | + | |
| - | {{Caja|contenido=<math>V=A_b \cdot h</math>}} | + | |
| - | |celda3={{p}} | + | |
| - | * '''Elementos:'''{{p}} | + | |
| - | :<math>A_b\;\!</math>: Área de la base. | + | |
| - | :<math>A_l\;\!</math>: Área lateral. | + | |
| - | :<math>P_b\;\!</math>: Perímetro de la base. | + | |
| - | :<math>h\;\!</math>: altura. | + | |
| - | }} | + | |
| - | {{p}} | + | |
| - | {{Geogebra_enlace | + | |
| - | |descripcion=En esta escena podrás ver el desarrollo de un prisma recto regular y calcular su volumen y sus áreas. | + | |
| - | |enlace=[https://ggbm.at/qkXa6fNp Desarrollo, áreas y volumen del prisma] | + | |
| - | }} | + | |
| {{p}} | {{p}} | ||
| ===Ortoedro=== | ===Ortoedro=== | ||
| Línea 59: | Línea 39: | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| + | |||
| ==Pirámide== | ==Pirámide== | ||
| {{Tabla3 | {{Tabla3 | ||
Revisión de 13:32 1 dic 2016
Tabla de contenidos |
Prisma
|
|
- 0:00-1:40: Definición de prisma recto.
- 1:30-4:12 :Superficie lateral del prisma recto.
- 4:12-5:12 :Superficie total del prisma recto.
- 5:12-6:09 :Volumen del prisma recto.
- 6:09-12:54: Problema: Halla el área lateral, el área total y el volumen de un prisma triangular regular de 5 cm de arista básica y 7 cm de altura.
Cálculo del área total y el volumen de un prisma. Ejemplos.
Área y volumen del prisma recto.
En este vídeo de MasterD, se pretende dejar claros todos los conceptos relacionados con los prismas. Daremos una definición, explicaremos cuáles son sus partes, veremos cómo se pueden clasificar con algunos ejemplos y finalmente pasaremos a ver el área y el volumen.
Cálculo del volumen y la superficie de un prisma.
Aviso: El vídeo habla de los cilindros como un caso especial de prisma aunque en realidad nisiquiera son poliedros. No obstante su volumen y superficie se obtienen de forma similar.
Halla el área y el volumen de un prisma recto de base triangular, sabiendo que la base es un triángulo rectángulo cuyos catetos miden 3 cm y 4 cm, y la altura mide 9 cm.
Imagina que te contrata una empresa de zumos para que diseñes un nuevo envase. Como el logotipo de la empresa es un hexágono, quieren que la forma del nuevo envase de zumo sea un prisma recto hexagonal. El envase debe caber en las estanterías del supermercado, por lo que te exigen que la altura sea 10 cm. Además quieren que quepa un litro de zumo, es decir, que el volumen del prisma sea 1 litro. ¿Cuánto debe medir el lado de la base?
Ejercicios para calcular el volumen y superficie de distintos prismas.
En esta escena podrás ver el desarrollo de un prisma recto regular y calcular su volumen y sus áreas.
Ortoedro
Como sabemos, un ortoedro es un prisma recto de base rectangular o cuadrada.
|
|
Cubo
Un caso particular de ortoedro es el cubo cuyas caras son todas cuadradas.
|
|
En esta escena podrás ver el desarrollo de un ortoedro y calcular su volumen y su área.
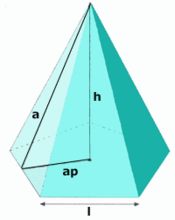
Pirámide
|
|
En esta escena podrás ver el desarrollo de una pirámide y calcular su volumen y su áreas.
Pirámide truncada
|
|
En esta escena podrás calcular el volumen y las áreas del tronco de pirámide.
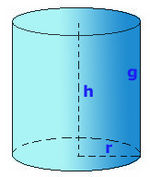
Cilindro
|
|
En esta escena podrás ver el desarrollo de un cilindro y calcular su volumen y sus áreas.
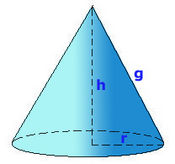
Cono
|
|
En esta escena podrás ver el desarrollo de un cono y calcular su volumen y sus áreas.
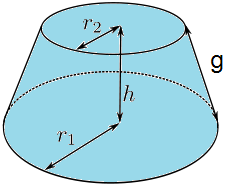
Cono truncado
|
|
En esta escena podrás calcular el volumen y las áreas de un tronco de cono.
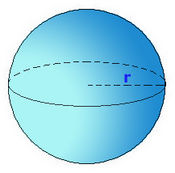
Esfera
|
|
En esta escena podrás calcular el volumen y área de un balón de futbol.
En esta escena podrás comprobar la relación que existe entre los volúmenes de la esfera, el cono y el cilindro.
Ejercicios
|
Actividad Interactiva: Volúmenes de cuerpos irregulares
Actividad 1. Halla el volumen de las siguientes figuras.
Actividad: Halla el volumen de las figuras que aparecen en la siguiente escena. Pulsa las flechas para cambiar la figura.
Actividad 2. Halla el volumen de las siguientes figuras.
Actividad: Halla el volumen de las figuras que aparecen en la siguiente escena. Pulsa las flechas para cambiar la figura. |
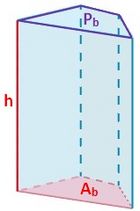
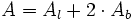
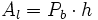
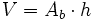
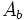 : Área de la base.
: Área de la base.
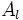 : Área lateral.
: Área lateral.
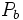 : Perímetro de la base.
: Perímetro de la base.
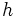 : altura.
: altura.
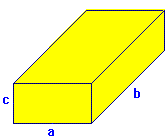
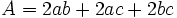
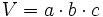
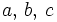 : aristas.
: aristas.
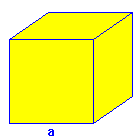
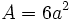
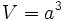
 : arista.
: arista.
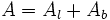
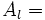 Suma áreas triángulos
Suma áreas triángulos
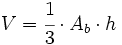
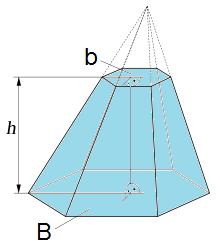
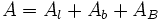
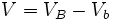
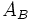 : Área de la base inferior.
: Área de la base inferior.
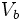 : Volumen de la pirámide pequeña de base b.
: Volumen de la pirámide pequeña de base b.
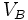 : Volumen de la pirámide completa de base B.
: Volumen de la pirámide completa de base B.
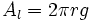
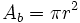
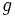 : generatriz.
: generatriz.
 : radio.
: radio.
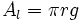
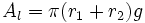
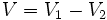
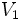 : Volumen del cono completo.
: Volumen del cono completo.
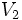 : Volumen del cono pequeño eliminado.
: Volumen del cono pequeño eliminado.