Plantilla:Prisma
De Wikipedia
| Revisión de 13:33 1 dic 2016 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 13:34 1 dic 2016 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 22: | Línea 22: | ||
| {{p}} | {{p}} | ||
| ===Ortoedro=== | ===Ortoedro=== | ||
| - | Como sabemos, un '''ortoedro''' es un prisma recto de base rectangular o cuadrada. | + | {{Ortoedro}} |
| - | + | ||
| - | {{Tabla3 | + | |
| - | |celda1= | + | |
| - | <center>[[Imagen:ortoedro.gif]]</center> | + | |
| - | |celda2={{p}} | + | |
| - | * '''Área:'''{{p}} | + | |
| - | {{Caja|contenido=<math>A=2ab+2ac+2bc\;\!</math>}}{{p}} | + | |
| - | * '''Volumen:'''{{p}} | + | |
| - | {{Caja|contenido=<math>V=a \cdot b \cdot c</math>}} | + | |
| - | |celda3={{p}} | + | |
| - | * '''Elementos:'''{{p}} | + | |
| - | :<math>a, \, b, \, c\;\!</math>: aristas. | + | |
| - | }} | + | |
| {{p}} | {{p}} | ||
| ===Cubo=== | ===Cubo=== | ||
Revisión de 13:34 1 dic 2016
|
|
En esta escena podrás ver el desarrollo de un prisma recto regular y calcular su volumen y sus áreas.
Ortoedro
Cómo medimos el volumen.
Medición de volumen con cubos unitarios.
Midiendo el volumen como área por longitud.
Cómo se obtiene el volumen de un ortoedro.
Halla el volumen de una caja de dimensiones 3 x 5 x 6 pies.
Un tanque de agua tiene 12 pies de alto, 5 pies de largo y 9 pies de ancho. Una caja sólida de metal con 7 pies de alto, 4 pies de largo y 8 pies de ancho yace al fondo del tanque. El tanque se llena con agua. ¿Cuál es el volumen de agua en el tanque?
Volumen de un prisma recto (ortoedro) de aristas 12.4, 8.5 y 6.2 cm.
Cálcula el área y el volumen de un prisma cuadrangular regular cuya arista básica mide 6.5 cm, y cuya altura es de 8.4 cm.
Calcula el volumen de una piscina de 50 m de largo, 21 m de ancho y 2 m de alto.
Cálcula el área de un ortoedro de aristas 4, 5, y 6 cm.
Actividades sobre volúmenes de ortoedros.
El volumen con cubos unitarios.
Volumen del ortoedro.
Problemas sobre volúmenes de ortoedros.
Actividades de autoevaluación sobre volúmenes de ortoedros.
Actividades de autoevaluación sobre volúmenes de ortoedros.
En esta escena podrás ver el desarrollo de un ortoedro y calcular su volumen y su área.
Cubo
Un caso particular de ortoedro es el cubo cuyas caras son todas cuadradas.
|
|
En esta escena podrás ver el desarrollo de un ortoedro y calcular su volumen y su área.
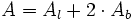
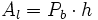
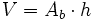
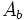 : Área de la base.
: Área de la base.
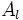 : Área lateral.
: Área lateral.
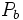 : Perímetro de la base.
: Perímetro de la base.
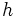 : altura.
: altura.
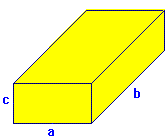
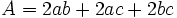
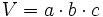
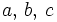 : aristas.
: aristas.
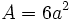
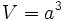
 : arista.
: arista.

