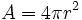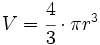Plantilla:Áreas y volúmenes en el espacio
De Wikipedia
| Revisión de 18:58 30 nov 2016 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión actual Coordinador (Discusión | contribuciones) (→Ejercicios) |
||
| Línea 1: | Línea 1: | ||
| ==Prisma== | ==Prisma== | ||
| - | {{Tabla3 | + | {{Prisma}} |
| - | |celda1= | + | |
| - | <center>[[Imagen:prisma.gif | 175px]]</center> | + | |
| - | |celda2={{p}} | + | |
| - | * '''Áreas:'''{{p}} | + | |
| - | {{Caja|contenido=<math>A=A_l+2 \cdot A_b </math>}}{{p}} | + | |
| - | {{Caja|contenido=<math>A_l=P_b \cdot h </math>}} | + | |
| - | * '''Volumen:'''{{p}} | + | |
| - | {{Caja|contenido=<math>V=A_b \cdot h</math>}} | + | |
| - | |celda3={{p}} | + | |
| - | * '''Elementos:'''{{p}} | + | |
| - | :<math>A_b\;\!</math>: Área de la base. | + | |
| - | :<math>A_l\;\!</math>: Área lateral. | + | |
| - | :<math>P_b\;\!</math>: Perímetro de la base. | + | |
| - | :<math>h\;\!</math>: altura. | + | |
| - | }} | + | |
| - | {{p}} | + | |
| - | {{Geogebra_enlace | + | |
| - | |descripcion=En esta escena podrás ver el desarrollo de un prisma recto regular y calcular su volumen y sus áreas. | + | |
| - | |enlace=[https://ggbm.at/qkXa6fNp Desarrollo, áreas y volumen del prisma] | + | |
| - | }} | + | |
| {{p}} | {{p}} | ||
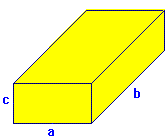
| ===Ortoedro=== | ===Ortoedro=== | ||
| - | Como sabemos, un '''ortoedro''' es un prisma recto de base rectangular o cuadrada. | + | {{Ortoedro}} |
| - | + | ||
| - | {{Tabla3 | + | |
| - | |celda1= | + | |
| - | <center>[[Imagen:ortoedro.gif]]</center> | + | |
| - | |celda2={{p}} | + | |
| - | * '''Área:'''{{p}} | + | |
| - | {{Caja|contenido=<math>A=2ab+2ac+2bc\;\!</math>}}{{p}} | + | |
| - | * '''Volumen:'''{{p}} | + | |
| - | {{Caja|contenido=<math>V=a \cdot b \cdot c</math>}} | + | |
| - | |celda3={{p}} | + | |
| - | * '''Elementos:'''{{p}} | + | |
| - | :<math>a, \, b, \, c\;\!</math>: aristas. | + | |
| - | }} | + | |
| {{p}} | {{p}} | ||
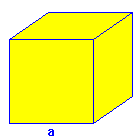
| ===Cubo=== | ===Cubo=== | ||
| - | Un caso particular de ortoedro es el '''cubo''' cuyas caras son todas cuadradas. | + | {{cubo}} |
| - | + | ||
| - | {{Tabla3 | + | |
| - | |celda1= | + | |
| - | <center>[[Imagen:cubo2.gif]]</center> | + | |
| - | |celda2={{p}} | + | |
| - | * '''Área:'''{{p}} | + | |
| - | {{Caja|contenido=<math>A=6a^2\;\!</math>}}{{p}} | + | |
| - | * '''Volumen:'''{{p}} | + | |
| - | {{Caja|contenido=<math>V=a^3\;\!</math>}} | + | |
| - | |celda3={{p}} | + | |
| - | * '''Elementos:'''{{p}} | + | |
| - | :<math>a\;\!</math>: arista. | + | |
| - | }} | + | |
| - | {{p}} | + | |
| - | {{Geogebra_enlace | + | |
| - | |descripcion=En esta escena podrás ver el desarrollo de un ortoedro y calcular su volumen y su área. | + | |
| - | |enlace=[https://ggbm.at/bEyWk8bY Desarrollo, área y volumen del ortoedro] | + | |
| - | }} | + | |
| - | {{p}} | + | |
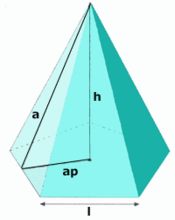
| ==Pirámide== | ==Pirámide== | ||
| - | {{Tabla3 | + | {{pirámide}} |
| - | |celda1= | + | |
| - | <center>[[Imagen:piramide.gif |175 px]]</center> | + | |
| - | |celda2={{p}} | + | |
| - | * '''Área:'''{{p}} | + | |
| - | {{Caja|contenido=<math>A=A_l+A_b \;\!</math>}}{{p}} | + | |
| - | {{Caja|contenido=<math>A_l=\;\!</math> Suma áreas triángulos}} | + | |
| - | * '''Volumen:'''{{p}} | + | |
| - | {{Caja|contenido=<math>V=\cfrac{1}{3} \cdot A_b \cdot h</math>}} | + | |
| - | |celda3={{p}} | + | |
| - | * '''Elementos:'''{{p}} | + | |
| - | :<math>A_b\;\!</math>: Área de la base. | + | |
| - | :<math>A_l\;\!</math>: Área lateral. | + | |
| - | :<math>h\;\!</math>: altura. | + | |
| - | }} | + | |
| - | {{p}} | + | |
| - | {{Geogebra_enlace | + | |
| - | |descripcion=En esta escena podrás ver el desarrollo de una pirámide y calcular su volumen y su áreas. | + | |
| - | |enlace=[https://ggbm.at/MNTfhgXA Desarrollo, áreas y volumen de la pirámide] | + | |
| - | }} | + | |
| {{p}} | {{p}} | ||
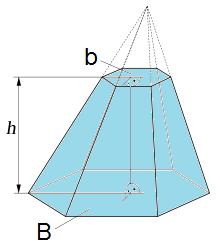
| ===Pirámide truncada=== | ===Pirámide truncada=== | ||
| - | {{Tabla3 | + | {{Pirámide truncada}} |
| - | |celda1= | + | |
| - | <center>[[Imagen:piramidetruncada.jpg]]</center> | + | |
| - | |celda2={{p}} | + | |
| - | * '''Área:'''{{p}} | + | |
| - | {{Caja|contenido=<math>A=A_l+A_b+A_B \;\!</math>}}{{p}} | + | |
| - | {{Caja|contenido=<math>A_l=\;\!</math> Suma áreas trapecios}} | + | |
| - | * '''Volumen:'''{{p}} | + | |
| - | {{Caja|contenido=<math>V=V_B-V_b\;\!</math>}} | + | |
| - | |celda3={{p}} | + | |
| - | * '''Elementos:'''{{p}} | + | |
| - | :<math>A_b\;\!</math>: Área de la base superior. | + | |
| - | :<math>A_B\;\!</math>: Área de la base inferior. | + | |
| - | :<math>A_l\;\!</math>: Área lateral. | + | |
| - | :<math>h\;\!</math>: altura. | + | |
| - | :<math>V_b\;\!</math>: Volumen de la pirámide pequeña de base b. | + | |
| - | :<math>V_B\;\!</math>: Volumen de la pirámide completa de base B. | + | |
| - | }} | + | |
| {{p}} | {{p}} | ||
| - | {{AI2|titulo=Actividad Interactiva: ''Tronco de pirámide''|cuerpo= | ||
| - | {{ai_cuerpo | ||
| - | |enunciado='''Actividad 1:''' Halla el volumen de un tronco de pirámide cuadrada que tiene una arista básica mayor de 3 cm, una arista básica menor de 2 cm y una altura de 1,7 cm. Halla también su superficie. | ||
| - | |actividad= | ||
| - | |||
| - | Comprueba los resultados en la siguiente escena: | ||
| - | |||
| - | <center><iframe> | ||
| - | url=http://maralboran.org/web_ma/descartes/1y2_eso/Volumenes_d3/VOLUMENES_9_1.html | ||
| - | width=840 | ||
| - | height=490 | ||
| - | name=myframe | ||
| - | </iframe></center> | ||
| - | <center>[http://maralboran.org/web_ma/descartes/1y2_eso/Volumenes_d3/VOLUMENES_9_1.html '''Shift-Click''' aquí si no se ve bien la escena]</center> | ||
| - | }} | ||
| - | }} | ||
| ==Cilindro== | ==Cilindro== | ||
| - | {{Tabla3 | + | {{Cilindro}} |
| - | |celda1= | + | |
| - | <center>[[Imagen:cilindro.jpg | 150 px]]</center> | + | |
| - | |celda2={{p}} | + | |
| - | * '''Área:'''{{p}} | + | |
| - | {{Caja|contenido=<math>A=A_l+2 \cdot A_b </math>}}{{p}} | + | |
| - | {{Caja|contenido=<math>A_l=2 \pi rg\;\!</math>}}{{p}} | + | |
| - | {{Caja|contenido=<math>A_b=\pi r^2\;\!</math>}} | + | |
| - | * '''Volumen:'''{{p}} | + | |
| - | {{Caja|contenido=<math>V=A_b \cdot h</math>}} | + | |
| - | |celda3={{p}} | + | |
| - | * '''Elementos:'''{{p}} | + | |
| - | :<math>A_b\;\!</math>: Área de la base. | + | |
| - | :<math>A_l\;\!</math>: Área lateral. | + | |
| - | :<math>h\;\!</math>: altura. | + | |
| - | :<math>g\;\!</math>: generatriz. | + | |
| - | :<math>r\;\!</math>: radio. | + | |
| - | }} | + | |
| - | {{p}} | + | |
| - | {{Geogebra_enlace | + | |
| - | |descripcion=En esta escena podrás ver el desarrollo de un cilindro y calcular su volumen y sus áreas. | + | |
| - | |enlace=[https://ggbm.at/BFHkAGXq Desarrollo, área y volumen del cilindro] | + | |
| - | }} | + | |
| {{p}} | {{p}} | ||
| + | |||
| ==Cono== | ==Cono== | ||
| - | {{Tabla3 | + | {{cono}} |
| - | |celda1= | + | |
| - | <center>[[Imagen:cono.jpg| 175 px]]</center> | + | |
| - | |celda2={{p}} | + | |
| - | * '''Área:'''{{p}} | + | |
| - | {{Caja|contenido=<math>A=A_l+A_b \;\!</math>}}{{p}} | + | |
| - | {{Caja|contenido=<math>A_l=\pi rg\;\!</math>}}{{p}} | + | |
| - | {{Caja|contenido=<math>A_b=\pi r^2\;\!</math>}} | + | |
| - | * '''Volumen:'''{{p}} | + | |
| - | {{Caja|contenido=<math>V=\cfrac{1}{3} \cdot A_b \cdot h</math>}} | + | |
| - | |celda3={{p}} | + | |
| - | * '''Elementos:'''{{p}} | + | |
| - | :<math>A_b\;\!</math>: Área de la base. | + | |
| - | :<math>A_l\;\!</math>: Área lateral. | + | |
| - | :<math>h\;\!</math>: altura. | + | |
| - | :<math>g\;\!</math>: generatriz. | + | |
| - | :<math>r\;\!</math>: radio. | + | |
| - | }} | + | |
| - | {{p}}{{p}} | + | |
| - | {{Geogebra_enlace | + | |
| - | |descripcion=En esta escena podrás ver el desarrollo de un cono y calcular su volumen y sus áreas. | + | |
| - | |enlace=[https://ggbm.at/PAA9APzE Desarrollo, áreas y volumen del cono] | + | |
| - | }} | + | |
| {{p}} | {{p}} | ||
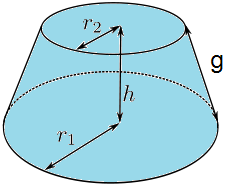
| ===Cono truncado=== | ===Cono truncado=== | ||
| - | {{Tabla3 | + | {{cono truncado}} |
| - | |celda1= | + | |
| - | <center>[[Imagen:conotruncado.gif]]</center> | + | |
| - | |celda2={{p}} | + | |
| - | * '''Área:'''{{p}} | + | |
| - | {{Caja|contenido=<math>A=A_l+\pi r_1^2+\pi r_2^2 \;\!</math>}}{{p}} | + | |
| - | {{Caja|contenido=<math>A_l=\pi (r_1+r_2)g\;\!</math>}}{{p}} | + | |
| - | * '''Volumen:'''{{p}} | + | |
| - | {{Caja|contenido=<math>V=V_1-V_2\;\!</math>}} | + | |
| - | |celda3={{p}} | + | |
| - | * '''Elementos:'''{{p}} | + | |
| - | :<math>A_l\;\!</math>: Área lateral. | + | |
| - | :<math>h\;\!</math>: altura. | + | |
| - | :<math>V_1\;\!</math>: Volumen del cono completo. | + | |
| - | :<math>V_2\;\!</math>: Volumen del cono pequeño eliminado. | + | |
| - | }} | + | |
| {{p}} | {{p}} | ||
| - | {{AI2|titulo=Actividad Interactiva: ''Tronco de cono''|cuerpo= | ||
| - | {{ai_cuerpo | ||
| - | |enunciado='''Actividad 1:''' Halla el volumen de un tronco de cono que tiene un radio básico mayor de 4,2 cm, un radio básico menor de 2 cm y una altura de 2 cm. Halla también su superficie. | ||
| - | |actividad= | ||
| - | |||
| - | Comprueba los resultados en la siguiente escena: | ||
| - | |||
| - | <center><iframe> | ||
| - | url=http://maralboran.org/web_ma/descartes/1y2_eso/Volumenes_d3/VOLUMENES_9_1.html | ||
| - | width=840 | ||
| - | height=490 | ||
| - | name=myframe | ||
| - | </iframe></center> | ||
| - | <center>[http://maralboran.org/web_ma/descartes/1y2_eso/Volumenes_d3/VOLUMENES_9_1.html '''Shift-Click''' aquí si no se ve bien la escena]</center> | ||
| - | }} | ||
| - | }} | ||
| ==Esfera== | ==Esfera== | ||
| - | {{Tabla3 | + | {{esfera}} |
| - | |celda1= | + | |
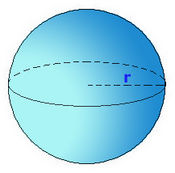
| - | <center>[[Imagen:esfera.jpg| 175 px]]</center> | + | |
| - | |celda2={{p}} | + | |
| - | * '''Área:'''{{p}} | + | |
| - | {{Caja|contenido=<math>A=4 \pi r^2 \;\!</math>}}{{p}} | + | |
| - | * '''Volumen:'''{{p}} | + | |
| - | {{Caja|contenido=<math>V=\cfrac{4}{3} \cdot \pi r^3</math>}} | + | |
| - | |celda3={{p}} | + | |
| - | * '''Elementos:'''{{p}} | + | |
| - | :<math>r\;\!</math>: radio. | + | |
| - | }} | + | |
| {{p}} | {{p}} | ||
| - | {{AI2|titulo=Actividades Interactivas: ''Volumen de la esfera''|cuerpo= | + | ==Ejercicios=={{p}} |
| - | {{ai_cuerpo | + | {{Geogebra_enlace |
| - | |enunciado='''Actividad 1:''' Halla el volumen de una esfera de 2,1 cm de radio. | + | |descripcion=En esta escena se te plantearán ejercicios de cálculo de volúmenes y áreas de cuerpos geométricos. |
| - | |actividad= | + | |enlace=[https://ggbm.at/qrQ8qwSM Autoevaluación: Volumen y superficie de cuerpos] |
| - | + | ||
| - | Comprueba los resultados en la siguiente escena: | + | |
| - | + | ||
| - | <center><iframe> | + | |
| - | url=http://maralboran.org/web_ma/descartes/1y2_eso/Volumenes_d3/VOLUMENES_6_1.html | + | |
| - | width=530 | + | |
| - | height=390 | + | |
| - | name=myframe | + | |
| - | </iframe></center> | + | |
| - | <center>[http://maralboran.org/web_ma/descartes/1y2_eso/Volumenes_d3/VOLUMENES_6_1.html '''Shift-Click''' aquí si no se ve bien la escena]</center> | + | |
| - | }} | + | |
| - | {{ai_cuerpo | + | |
| - | |enunciado='''Actividad 2:''' ¿Qué relación existe entre el volumen de la esfera y los volúmenes del cilindro y del cono? | + | |
| - | |actividad= | + | |
| - | + | ||
| - | En la siguiente escena modifica los valores del radio y observa los resultados: | + | |
| - | + | ||
| - | <center><iframe> | + | |
| - | url=http://maralboran.org/web_ma/descartes/1y2_eso/Volumenes_d3/VOLUMENES_6_2.html | + | |
| - | width=530 | + | |
| - | height=390 | + | |
| - | name=myframe | + | |
| - | </iframe></center> | + | |
| - | <center>[http://maralboran.org/web_ma/descartes/1y2_eso/Volumenes_d3/VOLUMENES_6_2.html '''Shift-Click''' aquí si no se ve bien la escena]</center> | + | |
| - | + | ||
| - | En consecuencia,si llamamos: | + | |
| - | + | ||
| - | *<math>V_c \;\!</math>= Volumen del cilindro de radio R y altura 2R | + | |
| - | *<math>V_e \;\!</math>= Volumen de la esfera de radio R. | + | |
| - | *<math>V_n \;\!</math>= Volumen del cono de radio R y altura 2R. | + | |
| - | + | ||
| - | entonces: | + | |
| - | + | ||
| - | *<math>V_e=2 \cdot V_n</math> | + | |
| - | *<math>V_c=3 \cdot V_n</math> | + | |
| - | *<math>V_c=V_n+V_e \;\!</math> | + | |
| - | }} | + | |
| - | {{ai_cuerpo | + | |
| - | |enunciado='''Actividad 3:''' Halla el volumen y la superficie de un balón de futbol. | + | |
| - | |actividad= | + | |
| - | [[Imagen:balon.jpg |left]] | + | |
| - | '''Balón Fútbol Competición, MASTER T-5:'''{{p}} | + | |
| - | Balón técnico para competición. Cubierta de cuero PU Cordley de 32 paneles cosidos. Fabricado bajo norma ISO9002 de acuerdo a las especificaciones FIFA. Sus cuatro capas de poliéster garantizan estabilidad y evitan la deformación del balón. Cámara de látex de doble laminado y válvula de Butyl automática. | + | |
| - | + | ||
| - | '''Datos técnicos:''' | + | |
| - | *Peso: 425-435 gr.{{p}} | + | |
| - | *Circunferencia: 68-70 cm | + | |
| - | {{p}} | + | |
| - | + | ||
| - | + | ||
| - | Con estos datos, calcula en tu cuaderno la superficie y el volumen y comprueba los resultados en la siguiente escena: | + | |
| - | + | ||
| - | <center><iframe> | + | |
| - | url=http://maralboran.org/web_ma/descartes/1y2_eso/Volumenes_d3/VOLUMENES_6_3.html | + | |
| - | width=530 | + | |
| - | height=350 | + | |
| - | name=myframe | + | |
| - | </iframe></center> | + | |
| - | <center>[http://maralboran.org/web_ma/descartes/1y2_eso/Volumenes_d3/VOLUMENES_6_3.html '''Shift-Click''' aquí si no se ve bien la escena]</center> | + | |
| - | }} | + | |
| - | + | ||
| - | }} | + | |
| - | {{p}} | + | |
| - | + | ||
| - | ==Ejercicios== | + | |
| - | {{AI2|titulo=Actividad Interactiva: ''Volúmenes de cuerpos irregulares''|cuerpo= | + | |
| - | {{ai_cuerpo | + | |
| - | |enunciado='''Actividad 1.''' Halla el volumen de las siguientes figuras. | + | |
| - | |actividad= | + | |
| - | Halla el volumen de las figuras que aparecen en la siguiente escena. Pulsa las flechas para cambiar la figura. | + | |
| - | {{p}} | + | |
| - | <center><iframe> | + | |
| - | url=http://maralboran.org/web_ma/descartes/1y2_eso/Volumenes_d3/VOLUMENES_8_1.html | + | |
| - | width=500 | + | |
| - | height=390 | + | |
| - | name=myframe | + | |
| - | </iframe></center> | + | |
| - | <center>[http://maralboran.org/web_ma/descartes/1y2_eso/Volumenes_d3/VOLUMENES_8_1.html '''Shift-Click''' aquí si no se ve bien la escena]</center> | + | |
| - | }} | + | |
| - | {{ai_cuerpo | + | |
| - | |enunciado='''Actividad 2.''' Halla el volumen de las siguientes figuras. | + | |
| - | |actividad= | + | |
| - | Halla el volumen de las figuras que aparecen en la siguiente escena. Pulsa las flechas para cambiar la figura. | + | |
| - | {{p}} | + | |
| - | <center><iframe> | + | |
| - | url=http://maralboran.org/web_ma/descartes/1y2_eso/Volumenes_d3/VOLUMENES_8_2.html | + | |
| - | width=500 | + | |
| - | height=390 | + | |
| - | name=myframe | + | |
| - | </iframe></center> | + | |
| - | <center>[http://maralboran.org/web_ma/descartes/1y2_eso/Volumenes_d3/VOLUMENES_8_2.html '''Shift-Click''' aquí si no se ve bien la escena]</center> | + | |
| - | }} | + | |
| - | + | ||
| }} | }} | ||
Revisión actual
Tabla de contenidos |
Prisma
|
|
- 0:00-1:40: Definición de prisma recto.
- 1:30-4:12 :Superficie lateral del prisma recto.
- 4:12-5:12 :Superficie total del prisma recto.
- 5:12-6:09 :Volumen del prisma recto.
- 6:09-12:54: Problema: Halla el área lateral, el área total y el volumen de un prisma triangular regular de 5 cm de arista básica y 7 cm de altura.
Cálculo del área total y el volumen de un prisma. Ejemplos.
Área y volumen del prisma recto.
En este vídeo de MasterD, se pretende dejar claros todos los conceptos relacionados con los prismas. Daremos una definición, explicaremos cuáles son sus partes, veremos cómo se pueden clasificar con algunos ejemplos y finalmente pasaremos a ver el área y el volumen.
Cálculo del volumen y la superficie de un prisma.
Aviso: El vídeo habla de los cilindros como un caso especial de prisma aunque en realidad nisiquiera son poliedros. No obstante su volumen y superficie se obtienen de forma similar.
Halla el área y el volumen de un prisma recto de base triangular, sabiendo que la base es un triángulo rectángulo cuyos catetos miden 3 cm y 4 cm, y la altura mide 9 cm.
Imagina que te contrata una empresa de zumos para que diseñes un nuevo envase. Como el logotipo de la empresa es un hexágono, quieren que la forma del nuevo envase de zumo sea un prisma recto hexagonal. El envase debe caber en las estanterías del supermercado, por lo que te exigen que la altura sea 10 cm. Además quieren que quepa un litro de zumo, es decir, que el volumen del prisma sea 1 litro. ¿Cuánto debe medir el lado de la base?
Ejercicios para calcular el volumen y superficie de distintos prismas.
En esta escena podrás ver el desarrollo de un prisma recto regular y calcular su volumen y sus áreas.
Ortoedro
Cómo medimos el volumen.
Medición de volumen con cubos unitarios.
Midiendo el volumen como área por longitud.
Cómo se obtiene el volumen de un ortoedro.
Halla el volumen de una caja de dimensiones 3 x 5 x 6 pies.
Un tanque de agua tiene 12 pies de alto, 5 pies de largo y 9 pies de ancho. Una caja sólida de metal con 7 pies de alto, 4 pies de largo y 8 pies de ancho yace al fondo del tanque. El tanque se llena con agua. ¿Cuál es el volumen de agua en el tanque?
Volumen de un prisma recto (ortoedro) de aristas 12.4, 8.5 y 6.2 cm.
Cálcula el área y el volumen de un prisma cuadrangular regular cuya arista básica mide 6.5 cm, y cuya altura es de 8.4 cm.
Calcula el volumen de una piscina de 50 m de largo, 21 m de ancho y 2 m de alto.
Cálcula el área de un ortoedro de aristas 4, 5, y 6 cm.
Actividades sobre volúmenes de ortoedros.
El volumen con cubos unitarios.
Volumen del ortoedro.
Problemas sobre volúmenes de ortoedros.
Actividades de autoevaluación sobre volúmenes de ortoedros.
Actividades de autoevaluación sobre volúmenes de ortoedros.
En esta escena podrás ver el desarrollo de un ortoedro y calcular su volumen y su área.
Cubo
Cálculo del área y volumen de un cubo
Halla el volumen de un cubo cuya superficie total es de 36 cm2.
María tiene una caja para guardar juguetes con forma de cubo cuya arista mide 60 cm. ¿Cuántos m2 de plástico se utilizaron para construirla?. ¿Qué volumen tiene en m3?
Actividades de autoevaluación sobre volúmenes de cubos.
Pirámide
En esta escena podrás ver el desarrollo de una pirámide y calcular su volumen y su áreas.
- Área y volumen de la pirámide.
- Ejercicios:
- a) Halla el volumen de una pirámide cuya base es un triángulo rectángulo de lados 6, 8 y 10, y cuya altura es igaul al perímetro de la base.
- b) Halla el área total de una pirámide cuadrangular regular de 4 m de arista básica y 6 m de apotema.
Cálculo del área total y el volumen de una pirámide. Ejemplos.
Videotutorial.
Cálculo del área total y el volumen de una pirámide. Ejemplos.
Halla el área y el volumen de un pirámide cuadrangular regular sabiendo que la apotema mide 11 cm y el lado de la base 7 cm.
Halla el área y el volumen de un pirámide hexagonal regular sabiendo que la arista básica mide 5 cm, la altura mide 12 cm y la apotema de la pirámide, 14 cm.
Halla el área de una pirámide regular con base cuadrada, de arista básica 10 cm y altura 12 cm.
Halla el área de una pirámide regular con base hexagonal, de arista básica 16 cm y arista lateral 28 cm.
Ejercicios para calcular volumen y superficie de distintas pirámides.
Propiedad
Si tenemos un prisma y una pirámide con la misma base y la misma altura, entonces el volumen del prisma es igual a tres veces el volumen de la pirámide.
Es evidente si comparamos las fórmulas de los volúmenes de ambas figuras.
Video que muestra de forma práctica cómo el volumen de un cubo es tres veces el volumen de una pirámide con la misma base y altura que las del cubo.
Relación entre el volumen de un prisma y una pirámide
http://mundogenial.comPirámide truncada
Videotutorial.
En esta escena podrás calcular el volumen y las áreas del tronco de pirámide.
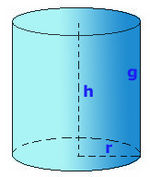
Cilindro
En esta escena podrás ver el desarrollo de un cilindro y calcular su volumen y sus áreas.
El cilindro:
- Definición.
- Elementos
- Área y volumen.
- Ejercicio.
Cálculo del área total y el volumen de un cilindro. Ejemplos.
Un camión cisterna tiene un depósito cilíndrico de 10 m de largo y bases de 2 m de diámetro. Calcula su capacidad en litros.
Calcula la altura de un cilindro de 825.19 cm3 de volumen y 6 cm de radio de la base.
En un depósito de gasolina de forma cilíndrica con una base de 3 m de diámetro y una profundidad de 12 m. Calcula el área total.
El área de la base de un cilindro es 25π cm2 y la generatriz es el doble del radio. Halla el volumen.
Si quieres cubrir un cilindro con tela, calcula el área de tela necesaria teniendo en cuenta que el cilindro mide 6 m de altura y 2 m de radio de la base.
Dos cilindros tienen la misma superficie lateral y sus radios miden 6 m y 8 m, respectivamente. Calcula sus alturas sabiendo que se diferencian en 3 m. Halla también sus superficies laterales.
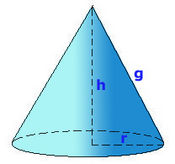
Cono
En esta escena podrás ver el desarrollo de un cono y calcular su volumen y sus áreas.
El cono:
- Definición.
- Elementos
- Área y volumen.
- Ejercicio.
Cálculo del área total y el volumen de un cono. Ejemplos.
Video que muestra de forma práctica cómo el volumen de un cilindro es tres veces el volumen de un cono con la misma base y altura que las del cilindro.
Un cono tiene una generatriz de 10 cm y una altura de 8 cm. Calcula su volumen.
Calcula el área total de un cono de 12 cm de diámetro y 8 cm de altura.
¿Cuánta cartulina necesitarás para realizar 25 conos de 20 cm de diámetro de la base y 60 cm de altura.
- Calcula el área total de un cono de 3 cm de radio y 4 cm de altura.
- Calcula el área total de un cono de 2 cm de radio y 7/8 cm de generatriz.
Calcula el área lateral de un cono de 30 cm de diámetro y 60 cm de altura.
Cono truncado
En esta escena podrás calcular el volumen y las áreas de un tronco de cono.
Esfera
En esta escena podrás calcular el volumen y área de un balón de futbol.
La esfera:
- Definición.
- Elementos
- Área y volumen.
- Ejercicio.
Cálculo del área total y el volumen ocupado por una esfera de radio r. Ejemplos.
Cálculo del área total y el volumen ocupado por una esfera de radio r. Ejemplos.
Halla el volumen y el área de una esfera de diámetro 10 cm.
Halla el radio de una esfera que tiene un volumen de 113.04 cm3.
Teorema
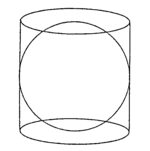
El volumen de la esfera es igual a dos tercios del volumen del cilindro circunscrito a ella.
El cálculo del volumen de la esfera fue uno de los descubrimientos que Arquímedes más estimaba de todos los que hizo en su vida. Llegó a demostrar de un modo muy original que el volumen de la esfera es igual a dos tercios del volumen del cilindro circular circunscrito a ella. Tanto le impresionó esto a él mismo que mandó que en su tumba se grabase esta figura en recuerdo de la mejor de sus ideas.
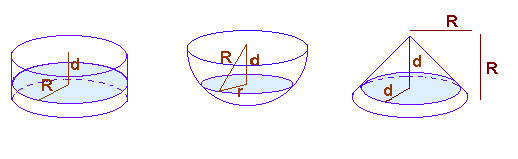
La siguiente no es una demostración rigurosa, sino intuitiva. Vamos a ver cómo llegó hasta ahí. Arquímedes se imaginó una semiesfera y junto a ella un cilindro circular recto y un cono recto, ambos de base igual a un círculo máximo de la semiesfera:
Arquímedes cortó las tres figuras por un plano paralelo a la base del cilindro y cono y se preguntó cómo serían las secciones determinadas por este plano en cilindro, semiesfera y cono. En el cilindro es un círculo de radio R. En la esfera también será un círculo, pero su radio dependerá de la distancia d. Mirando la figura y acordándote del teorema de Pitágoras, fácilmente puedes escribir que si el radio de la sección es r, entonces
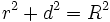
En el cono la sección también será un círculo y ahora el radio es aún más fácil de determinar (como el radio de apertura del cono es de 45º, resulta que el radio es d).
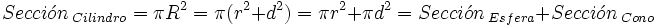
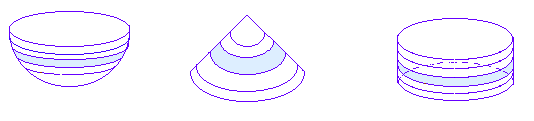
Las secciones son como rebanadas de las tres figuras obtenidas cortando paralelamente a la base del cilindro. Resulta que, colocando las tres figuras como las hemos puesto y cortándolas en rebanadas finas
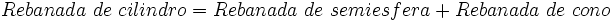 (a la misma altura)
(a la misma altura)Si para cada altura se tiene esta relación, parece bastante claro que:
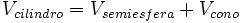
Pero como:
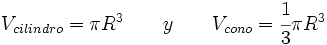
resulta:
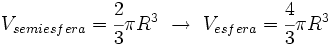
Corolario
El volumen de la semiesfera más el volumen de cono inscrito en ella es igual al volumen del cilindro circunscrito a ella.
|
|
Se ha visto en la demostración del teorema anterior
En esta escena podrás comprobar la relación que existe entre los volúmenes de la esfera, el cono y el cilindro.
En esta escena se te plantearán ejercicios de cálculo de volúmenes y áreas de cuerpos geométricos.
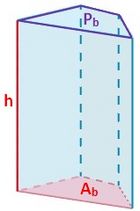
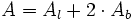
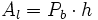
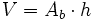
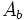 : Área de la base.
: Área de la base.
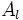 : Área lateral.
: Área lateral.
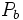 : Perímetro de la base.
: Perímetro de la base.
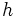 : altura.
: altura.
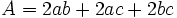
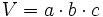
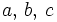 : aristas.
: aristas.
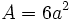
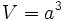
 : arista.
: arista.
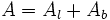
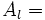 Suma áreas triángulos
Suma áreas triángulos
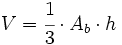

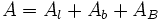
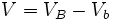
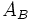 : Área de la base inferior.
: Área de la base inferior.
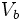 : Volumen de la pirámide pequeña de base b.
: Volumen de la pirámide pequeña de base b.
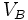 : Volumen de la pirámide completa de base B.
: Volumen de la pirámide completa de base B.
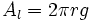
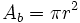
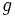 : generatriz.
: generatriz.
 : radio.
: radio.
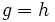
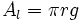
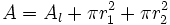
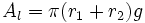
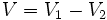
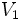 : Volumen del cono completo.
: Volumen del cono completo.
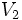 : Volumen del cono pequeño eliminado.
: Volumen del cono pequeño eliminado.