Funciones: Introducción (1ºBach)
De Wikipedia
| Revisión de 19:17 30 sep 2014 Coordinador (Discusión | contribuciones) (→Las funciones describen fenómenos reales) ← Ir a diferencia anterior |
Revisión de 14:02 3 dic 2016 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 7: | Línea 7: | ||
| {{p}} | {{p}} | ||
| ==Introducción== | ==Introducción== | ||
| + | {{Caja_Amarilla|texto= | ||
| + | El '''análisis matemático''' es una rama de las matemáticas que estudia los números reales, los complejos y las '''funciones''' entre esos conjuntos. Se empieza a desarrollar a partir de de la formulación rigurosa de '''límite''' y estudia conceptos como la '''continuidad''', la '''integración''' y la '''derivación'''. | ||
| + | }} | ||
| + | Una de las diferencias entre el álgebra y el análisis es que en este segundo recurre a construcciones que involucran sucesiones de un número infinito de elementos, mientras que álgebra usualmente es finitista. | ||
| + | }} | ||
| {{Video_enlace2 | {{Video_enlace2 | ||
| |titulo1=Fijando ideas | |titulo1=Fijando ideas | ||
| Línea 14: | Línea 19: | ||
| |url1=http://matematicasbachiller.com/videos/1-bachillerato/matematicas-de-primero-de-bachillerato/15-funciones-reales-de-variable-real/01-fijando-ideas-sobre-el-calculo-diferencial-de-una-variable#.VCr__xa7ZV8 | |url1=http://matematicasbachiller.com/videos/1-bachillerato/matematicas-de-primero-de-bachillerato/15-funciones-reales-de-variable-real/01-fijando-ideas-sobre-el-calculo-diferencial-de-una-variable#.VCr__xa7ZV8 | ||
| }} | }} | ||
| + | ==Una breve historia de las funciones== | ||
| + | En las matemáticas actuales el concepto de función se define del modo siguiente: | ||
| + | |||
| + | {{Caja_Amarilla|texto= | ||
| + | Sean A y B conjuntos. Se llama '''función''' entre A y B a cualquier relación establecida entre los elementos de A y B de tal modo que a cada elemento de A le corresponde un único elemento de B. | ||
| + | |||
| + | Para representar las funciones se suele utilizar la notación <math>f:A \rightarrow B</math> para los conjuntos, y=f(x) para los elementos. | ||
| + | |||
| + | A se llama '''conjunto inicial''' y B es el '''conjunto final'''. | ||
| + | }} | ||
| + | |||
| + | Se pueden definir funciones entre cualquier tipo de conjuntos, pero las más interesantes son las que se establecen entre conjuntos de números. En los próximos temas vamos a estudiar funciones definidas en el conjunto de los números reales: las funciones reales (conjunto final) | ||
| + | de variable real (conjunto inicial), <math>f:\mathbb{R} \rightarrow \mathbb{R}</math>. | ||
| + | |||
| + | La pregunta que cabe hacerse ahora es: ¿cómo se ha llegado hasta aquí?. Es importante entender que el concepto se desarrolló con el paso del tiempo; su significado fue cambiando y también la forma en que se definía, ganando precisión a través de los años. | ||
| + | |||
| + | Comenzaremos en Mesopotamia. En las matemáticas babilónicas encontramos tablas con los cuadrados, los cubos y los inversos de los | ||
| + | números naturales. Estas tablas sin duda definen funciones de <math>\mathbb{N}</math> en <math>\mathbb{N}</math> o de <math>\mathbb{N}</math> en <math>\mathbb{R}</math>, lo que no implica que los babilonios conocieran el concepto de función. Conocían y | ||
| + | manejaban funciones específicas, pero no el concepto abstracto y moderno de función. | ||
| + | |||
| ==Las funciones describen fenómenos reales== | ==Las funciones describen fenómenos reales== | ||
Revisión de 14:02 3 dic 2016
| Enlaces internos | Para repasar o ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadoras |
Introducción
El análisis matemático es una rama de las matemáticas que estudia los números reales, los complejos y las funciones entre esos conjuntos. Se empieza a desarrollar a partir de de la formulación rigurosa de límite y estudia conceptos como la continuidad, la integración y la derivación.
Una de las diferencias entre el álgebra y el análisis es que en este segundo recurre a construcciones que involucran sucesiones de un número infinito de elementos, mientras que álgebra usualmente es finitista. }}
- Introducción al cálculo diferencial.
Una breve historia de las funciones
En las matemáticas actuales el concepto de función se define del modo siguiente:
Sean A y B conjuntos. Se llama función entre A y B a cualquier relación establecida entre los elementos de A y B de tal modo que a cada elemento de A le corresponde un único elemento de B.
Para representar las funciones se suele utilizar la notación 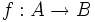 para los conjuntos, y=f(x) para los elementos.
para los conjuntos, y=f(x) para los elementos.
A se llama conjunto inicial y B es el conjunto final.
Se pueden definir funciones entre cualquier tipo de conjuntos, pero las más interesantes son las que se establecen entre conjuntos de números. En los próximos temas vamos a estudiar funciones definidas en el conjunto de los números reales: las funciones reales (conjunto final)
de variable real (conjunto inicial), 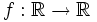 .
.
La pregunta que cabe hacerse ahora es: ¿cómo se ha llegado hasta aquí?. Es importante entender que el concepto se desarrolló con el paso del tiempo; su significado fue cambiando y también la forma en que se definía, ganando precisión a través de los años.
Comenzaremos en Mesopotamia. En las matemáticas babilónicas encontramos tablas con los cuadrados, los cubos y los inversos de los
números naturales. Estas tablas sin duda definen funciones de 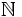 en
en 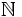 o de
o de 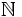 en
en  , lo que no implica que los babilonios conocieran el concepto de función. Conocían y
manejaban funciones específicas, pero no el concepto abstracto y moderno de función.
, lo que no implica que los babilonios conocieran el concepto de función. Conocían y
manejaban funciones específicas, pero no el concepto abstracto y moderno de función.

