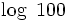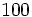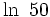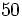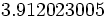Plantilla:Funciones logarítmicas (1ºBach)
De Wikipedia
| Revisión de 19:07 8 dic 2016 Coordinador (Discusión | contribuciones) (→Función logarítmica de base a) ← Ir a diferencia anterior |
Revisión actual Coordinador (Discusión | contribuciones) (→Propiedades) |
||
| Línea 3: | Línea 3: | ||
| {{p}} | {{p}} | ||
| ===Propiedades=== | ===Propiedades=== | ||
| - | {{Teorema_sin_demo|titulo=Propiedades de la función logarítmica|enunciado=Las funciones exponenciales de base <math>a\;</math> cumplen las siguientes propiedades: | + | {{Propiedades de la funcion logaritmica}} |
| - | + | ||
| - | *Son continuas en <math>\mathbb{R}{}_*^+</math>. | + | |
| - | *Pasan por <math>(1,0)\;</math> y <math>(a,1)\;</math>. | + | |
| - | *Si <math>a>1\;</math> son crecientes y si <math>0<a<1\;</math> son decrecientes. | + | |
| - | *Su crecimiento es menor que el de las funciones raíz de cualquier índice <math>\sqrt[n]{x}</math>. | + | |
| - | *La función logaritmica y la exponencial de la misma base son funciones inversas y por tanto sus gráficas son simétricas respecto de la recta <math>y=x\;</math>. | + | |
| - | }} | + | |
| - | {{p}} | + | |
| - | {{AI2|titulo=Actividad Interactiva: ''Propiedades de la función logar´tmica''|cuerpo= | + | |
| - | {{ai_cuerpo | + | |
| - | |enunciado='''Actividad 1.''' Comprueba las propiedades de las funciones logarítmicas en la siguiente escena. | + | |
| - | |actividad= | + | |
| - | + | ||
| - | <center><iframe> | + | |
| - | url=http://maralboran.org/web_ma/geogebra/figuras/logaritmica_1.html | + | |
| - | width=780 | + | |
| - | height=460 | + | |
| - | name=myframe | + | |
| - | </iframe></center> | + | |
| - | <center>[http://maralboran.org/web_ma/geogebra/figuras/logaritmica_1.html '''Click''' aquí si no se ve bien la escena]</center> | + | |
| - | {{p}} | + | |
| - | + | ||
| - | Comprueba en la escena anterior las siguientes propiedades: | + | |
| - | + | ||
| - | * Todas pasan por los punto <math>(1,0)\;</math> y <math>(a,1)\;</math>, donde <math>a\;</math> es la base. | + | |
| - | * Si la base <math>a>1\;</math>, son crecientes y si <math>0<a<1\;</math> decrecientes. | + | |
| - | * Observa como varía la gráfica al aumentar o disminuir el valor de la base. | + | |
| - | * Las gráficas son simétricas respecto de la recta <math>y=x</math> (en rojo). | + | |
| - | + | ||
| - | Contesta: | + | |
| - | + | ||
| - | *¿Cuál es el dominio de estas funciones? o, lo que es lo mismo, ¿qué valores puede tomar la primera coordenada del punto azul? | + | |
| - | *¿Cuál es la imagen de estas funciones? o, lo que es lo mismo, ¿qué valores puede tomar la segunda coordenada del punto azul? | + | |
| - | *¿Cuál es el punto de corte de la gráfica con los ejes? | + | |
| - | }} | + | |
| - | }} | + | |
| - | }} | + | |
| {{p}} | {{p}} | ||
Revisión actual
Tabla de contenidos |
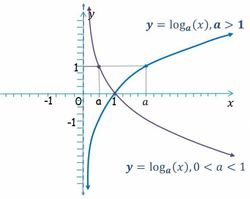
Función logarítmica de base a
Sea 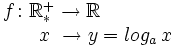
|
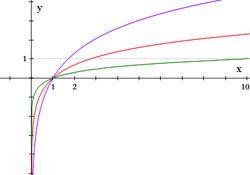
Propiedades
Propiedades de la función logarítmica Las funciones exponenciales de base
|
El modelo logarítmico
Ejemplo: Modelo logarítmico
Los científicos modelan la respuesta humana a estímulos (como sonido, luz o presión) por medio de funciones logarítmicas. El psicólogo Gustav Fechner formuló la ley como
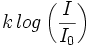
donde 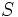 es la intensidad subjetiva del estímulo,
es la intensidad subjetiva del estímulo, 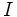 la intensida física del estímulo,
la intensida física del estímulo, 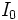 la intensidad física umbral y
la intensidad física umbral y  es una constante que difiere en cada estímulo sensorial.
es una constante que difiere en cada estímulo sensorial.
Por ejemplo, la percepción de la sonoridad 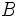 , en decibelios (dB), de un sonido con intensidad física
, en decibelios (dB), de un sonido con intensidad física 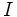 en W / m2 está dada por
en W / m2 está dada por
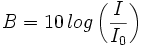
donde 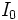 la intensidad física de un sonido apenas audible (umbral). Encuentra el nivel de sonoridad (en dB) de un sonido cuya intensidad física
la intensidad física de un sonido apenas audible (umbral). Encuentra el nivel de sonoridad (en dB) de un sonido cuya intensidad física 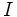 es 100 veces la de
es 100 veces la de 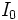 .
.
Partimos del hecho de que 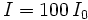 , entonces, sustituyendo en la fórmula de la percepción sonora, tendremos:
, entonces, sustituyendo en la fórmula de la percepción sonora, tendremos:
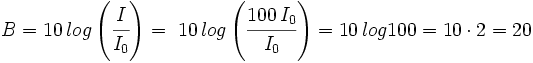
Calculadora
Logartitmo decimal
|
Calculadora: Logaritmo decimal |
Logartitmo neperiano
|
Calculadora: Logaritmo neperiano |
 . Se define la función logarítmica de base
. Se define la función logarítmica de base  como:
como:
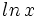 .
.
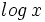 (sin especificar la base).
(sin especificar la base).
 .
.
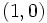 y
y 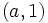 .
.
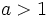 son crecientes.
son crecientes.
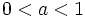 son decrecientes.
son decrecientes.
![\sqrt[n]{x}](/wikipedia/images/math/5/e/4/5e4352778f3b156f05ef056f9793ec36.png) .
.
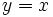 .
.