Plantilla:Funcion exponencial de base a
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 18:54 8 dic 2016 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 20:06 8 dic 2016 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 1: | Línea 1: | ||
| - | |||
| {{Tabla75|celda2=[[Imagen:Exponencial.png|center|thumb|Función exponencial de base 2]]|celda1= | {{Tabla75|celda2=[[Imagen:Exponencial.png|center|thumb|Función exponencial de base 2]]|celda1= | ||
| {{Caja_Amarilla | {{Caja_Amarilla | ||
| Línea 18: | Línea 17: | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| - | {{AI2|titulo=Actividad Interactiva: ''Función exponencial''|cuerpo= | + | {{Geogebra_enlace |
| - | {{ai_cuerpo | + | |descripcion=Representación de la familia de funciones exponenciales. |
| - | |enunciado='''Actividad 1.''' Representación gráfica de distintas funciones exponenciales. | + | |enlace=[https://ggbm.at/p7AhTQRd La función exponencial] |
| - | |actividad= | + | |
| - | En esta escena tienes las gráfica de las funciones: | + | |
| - | {{p}} | + | |
| - | <center>'''a)''' <math>y = 2^x\;</math> (en verde);{{b4}}'''b)''' <math>y = 3^x\;</math> (en amarillo);{{b4}}'''c)''' <math>y = \left ( \frac{1}{2} \right )^x</math> (en rojo);{{b4}}'''d)''' <math>y = \left ( \frac{1}{3} \right )^x</math> (en turquesa)</center> | + | |
| - | {{p}} | + | |
| - | Observa que las gráficas a) y c) son simétricas respecto del eje Y. Lo mismo ocurre con b) y d). | + | |
| - | + | ||
| - | + | ||
| - | <center><iframe> | + | |
| - | url=http://maralboran.org/web_ma/descartes/Analisis/El_pinta_graficas/grafic_4h.html | + | |
| - | width=450 | + | |
| - | height=380 | + | |
| - | name=myframe | + | |
| - | </iframe></center> | + | |
| - | <center>[http://maralboran.org/web_ma/descartes/Analisis/El_pinta_graficas/grafic_4h.html '''Click''' aquí si no se ve bien la escena]</center> | + | |
| - | {{p}} | + | |
| - | + | ||
| - | Prueba a cambiar también las funciones por otras. No olvides pulsar "Intro" al cambiar cada función. | + | |
| - | }} | + | |
| }} | }} | ||
Revisión de 20:06 8 dic 2016
Se define la función exponencial de base 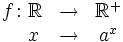 donde La función exponencial de base |  |
como:
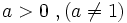es un número real.
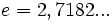(número e) es de especial importancia en matemáticas y se denomina simplementre función exponencial, sin hacer mención a la base.
La función exponencial Descripción: Representación de la familia de funciones exponenciales.
