Plantilla:Crecimiento exponencial
De Wikipedia
| Revisión de 20:27 8 dic 2016 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 20:28 8 dic 2016 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 25: | Línea 25: | ||
| {{p}} | {{p}} | ||
| {{Desplegable|titulo=Ejemplos:|contenido= | {{Desplegable|titulo=Ejemplos:|contenido= | ||
| - | *'''El ajedrez y los granos de trigo''' | + | *'''La leyenda del ajedrez''' |
| Una conocida leyenda oriental ofrece una descripción muy exacta de una función exponencial. Cuentan que un rey quiso premiar las dotes adivinatorias del sumo sacerdote que había predicho una extraordinaria victoria en una batalla. El sacerdote pidió 2 granos de trigo por la primera casilla de un tablero de ajedrez, 4 por la segunda, 8 por la tercera, y el doble cada vez por cada nueva casilla. El rey pareció complacido por la modestia del sacerdote... hasta que comprobó la magnitud de su petición. El número de granos de trigo era: | Una conocida leyenda oriental ofrece una descripción muy exacta de una función exponencial. Cuentan que un rey quiso premiar las dotes adivinatorias del sumo sacerdote que había predicho una extraordinaria victoria en una batalla. El sacerdote pidió 2 granos de trigo por la primera casilla de un tablero de ajedrez, 4 por la segunda, 8 por la tercera, y el doble cada vez por cada nueva casilla. El rey pareció complacido por la modestia del sacerdote... hasta que comprobó la magnitud de su petición. El número de granos de trigo era: | ||
| Línea 32: | Línea 32: | ||
| una cantidad inimaginable, que no se almacenaba en todo el reino. | una cantidad inimaginable, que no se almacenaba en todo el reino. | ||
| - | Los sumandos de esta expresión responderían, en la notación matemática actual, a la función <math>2^x\;</math>, para el dominio x = 1, 2, 3, ..., 64. | + | Los sumandos de esta expresión respondenr a la función <math>2^x\;</math>, para valores de x = 1, 2, 3, ..., 64. |
| *'''El interés compuesto e interés continuo''' | *'''El interés compuesto e interés continuo''' | ||
Revisión de 20:28 8 dic 2016
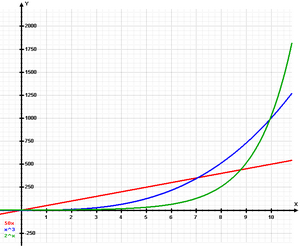
El término crecimiento exponencial se aplica generalmente a una magnitud 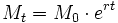 Donde:
Esta expresión también podemos ponerla como una función exponencial de base 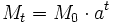 |
- La leyenda del ajedrez
Una conocida leyenda oriental ofrece una descripción muy exacta de una función exponencial. Cuentan que un rey quiso premiar las dotes adivinatorias del sumo sacerdote que había predicho una extraordinaria victoria en una batalla. El sacerdote pidió 2 granos de trigo por la primera casilla de un tablero de ajedrez, 4 por la segunda, 8 por la tercera, y el doble cada vez por cada nueva casilla. El rey pareció complacido por la modestia del sacerdote... hasta que comprobó la magnitud de su petición. El número de granos de trigo era:
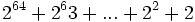
una cantidad inimaginable, que no se almacenaba en todo el reino.
Los sumandos de esta expresión respondenr a la función 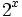 , para valores de x = 1, 2, 3, ..., 64.
, para valores de x = 1, 2, 3, ..., 64.
- El interés compuesto e interés continuo
El capital obtenido de la inversión de un capital inicial 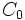 a un interés compuesto
a un interés compuesto  en
en  periodos anuales sigue la fórmula:
periodos anuales sigue la fórmula:
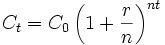
siendo 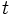 el tiempo transcurrido desde el inicio de la inversión.
el tiempo transcurrido desde el inicio de la inversión.
Se llama interés continuo a una inversión de este tipo en la que se considera que los intervalos de tiempo son cada vez más pequeños, hasta que la acumulación de intereses es instantánea. La fórmula del interés continuo es de tipo exponencial:
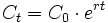
- Desintegración radiactiva
Las sustancias radiactivas se desintegran paulatinamente transformándose en otras clases de átomos y emitiendo energía y radiaciones ionizantes. La ley de desintegración radiactiva es de tipo exponencial decreciente, de manera que si 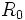 es la cantidad inicial de sustancia y
es la cantidad inicial de sustancia y  la constante de desintegración asociada al elemento químico, la cantidad remanente al cabo de un tiempo
la constante de desintegración asociada al elemento químico, la cantidad remanente al cabo de un tiempo 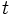 será:
será:
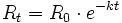
- Crecimiento demográfico
Las curvas de crecimiento vegetativo de una población, establecido como la diferencia entre nacimientos y muertes para un intervalo de tiempo dado, siguen una ley exponencial. siendo 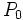 la población inicial e
la población inicial e 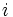 el índice de crecimiento anual en tanto por uno, y se considera una tasa de crecimiento continuo, la población seguirá la ley exponencial:
el índice de crecimiento anual en tanto por uno, y se considera una tasa de crecimiento continuo, la población seguirá la ley exponencial:
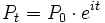
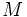 que crece con el tiempo
que crece con el tiempo 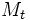 es valor de la magnitud en el instante
es valor de la magnitud en el instante 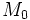 es el valor inicial de la variable, valor en
es el valor inicial de la variable, valor en 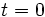 , cuando empezamos a medirla;
, cuando empezamos a medirla;
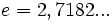 (número e)
(número e)
 haciendo
haciendo 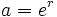 .
.