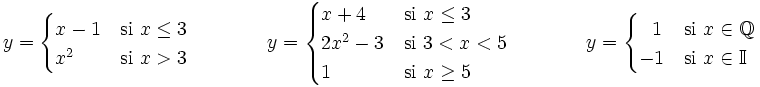Plantilla:Funciones definidas a trozos
De Wikipedia
| Revisión de 18:00 11 dic 2016 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 18:27 11 dic 2016 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 7: | Línea 7: | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| - | {{Ejemplo|titulo=Ejemplos: ''Funciones definidas a trozos'' | + | {{Ejemplo|titulo=Ejemplos: ''Función definida a trozos'' |
| - | |enunciado=Representa las siguientes funciones: | + | |enunciado=Representa la siguiente función: |
| - | '''a)''' <math>y = \begin{cases} x-3 & \mbox{si }x \le 0 \\ ~~2 & \mbox{si }0<x<3 \\ -x & \mbox{si }x \ge 3 \end{cases}</math> | + | <center><math>y = \begin{cases} x^2 & \mbox{si }x \le 1 \\ 2x+1 & \mbox{si }x>1 \end{cases}</math></center> |
| - | {{b4}}{{b4}} | + | |
| - | '''b)''' <math>y = \begin{cases} x^2 & \mbox{si }x \le 1 \\ 2x+1 & \mbox{si }x>1 \end{cases}</math> | + | |
| |sol= | |sol= | ||
| Para su representación, tenemos que dibujar cada una de las funciones en sus respectivos tramos, prestando especial atención a los puntos de "empalme" (extremos de los intervalos de definición). | Para su representación, tenemos que dibujar cada una de las funciones en sus respectivos tramos, prestando especial atención a los puntos de "empalme" (extremos de los intervalos de definición). | ||
| - | a) | + | [[Imagen:f_a_trozos_1.jpg|300px|center]] |
| - | {{Tabla50|celda2=[[Imagen:funcion_trozos.png|250px|center]] | + | }} |
| - | |celda1= | + | {{p}} |
| - | + | {{Ejemplo|titulo=Ejemplos: ''Función definida a trozos'' | |
| - | {{b}} | + | |enunciado=Encuentra la expresión analítica de la función cuya gráfica es la siguiente: |
| + | [[Imagen:funcion_trozos.png|250px|center]] | ||
| + | |sol= | ||
| + | Tendremos que hallar las ecuaciones de tres rectas. Para ello localizaremos dos puntos por los que pase cada recta y a partir de ellos obtendremos su ecuación. | ||
| + | {{p}} | ||
| <center><math>y = \begin{cases} x-3 & \mbox{si }x \le 0 \\ ~~2 & \mbox{si }0<x<3 \\ -x & \mbox{si }x \ge 3 \end{cases}</math></center> | <center><math>y = \begin{cases} x-3 & \mbox{si }x \le 0 \\ ~~2 & \mbox{si }0<x<3 \\ -x & \mbox{si }x \ge 3 \end{cases}</math></center> | ||
| - | }} | ||
| - | b) | ||
| - | {{Tabla50|celda2=[[Imagen:f_a_trozos_1.jpg|300px|center]] | ||
| - | |celda1= | ||
| - | |||
| - | {{b}} | ||
| - | |||
| - | <center><math>y = \begin{cases} x^2 & \mbox{si }x \le 1 \\ 2x+1 & \mbox{si }x>1 \end{cases}</math></center> | ||
| - | }} | ||
| }} | }} | ||
Revisión de 18:27 11 dic 2016
Una función definida a trozos es aquella que utiliza varias expresiones para su definición, utilizando cada una de ellas en un determinado tramo del dominio de definición de la función principal.
Son funciones definidas a trozos:
Ejemplos: Función definida a trozos
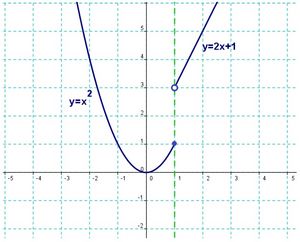
Representa la siguiente función:
Para su representación, tenemos que dibujar cada una de las funciones en sus respectivos tramos, prestando especial atención a los puntos de "empalme" (extremos de los intervalos de definición).
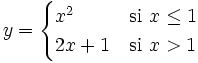
Ejemplos: Función definida a trozos
Encuentra la expresión analítica de la función cuya gráfica es la siguiente:
Tendremos que hallar las ecuaciones de tres rectas. Para ello localizaremos dos puntos por los que pase cada recta y a partir de ellos obtendremos su ecuación.
Función definida a trozos Descripción: En esta escena podrás representar funciones definidas en hasta 4 trozos.
