Plantilla:Transformaciones elementales de funciones (1ºBach)
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 19:28 12 dic 2016 Coordinador (Discusión | contribuciones) (→Actividades) ← Ir a diferencia anterior |
Revisión de 19:34 12 dic 2016 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 1: | Línea 1: | ||
| - | ==Traslación vertical== | + | ==Traslación vertical y horizontal== |
| - | {{Caja_Amarilla|texto=Sea <math>f(x)\;</math> una función y <math>k>0\;</math> un número real, entonces la gráfica de la función <math>f(x)+k\;</math> se obtiene a partir de la de <math>f(x)\;</math> desplazándola <math>k\;</math> unidades hacia arriba y la de <math>f(x)-k\;</math> desplazándola <math>k\;</math> unidades hacia abajo.}} | + | {{Caja_Amarilla|texto=*'''Traslación vertical:''' Sea <math>f(x)\;</math> una función y <math>k>0\;</math> un número real, entonces la gráfica de la función <math>f(x)+k\;</math> se obtiene a partir de la de <math>f(x)\;</math> desplazándola <math>k\;</math> unidades hacia arriba y la de <math>f(x)-k\;</math> desplazándola <math>k\;</math> unidades hacia abajo. |
| {{p}} | {{p}} | ||
| - | {{AI2|titulo=Actividad Interactiva: ''Traslación vertical de una función''|cuerpo= | + | *'''Traslación horizontal:''' Sea <math>f(x)\;</math> una función y <math>k>0\;</math> un número real, entonces la gráfica de la función <math>f(x+k)\;</math> se obtiene a partir de la de <math>f(x)\;</math> desplazándola <math>k\;</math> unidades hacia la izquierda y la de <math>f(x-k)\;</math> desplazándola <math>k\;</math> unidades hacia la derecha.}} |
| - | {{ai_cuerpo | + | |
| - | |enunciado='''Actividad 1.''' Representación gráfica de una función <math>f(x)\;</math> cualquiera y de su transformada <math>f(x) \pm k</math>. | + | |
| - | |actividad= | + | |
| - | En esta escena tienes la gráfica de la función <math>f(x) = x^2\;</math> (en verde) y la de <math>f(x)+1=x^2+1\;</math> (en amarillo). | + | |
| - | + | ||
| {{p}} | {{p}} | ||
| - | <center><iframe> | + | ==Simetría respecto de los ejes== |
| - | url=http://maralboran.org/web_ma/descartes/Analisis/El_pinta_graficas/grafic_4a.html | + | {{Caja_Amarilla|texto=*'''Simetría respecto del eje X:''' Las gráficas de las funciones <math>f(x)\;</math> y <math>-f(x)\;</math> son simétricas respecto del eje de abscisas. |
| - | width=450 | + | |
| - | height=380 | + | |
| - | name=myframe | + | |
| - | </iframe></center> | + | |
| - | <center>[http://maralboran.org/web_ma/descartes/Analisis/El_pinta_graficas/grafic_4a.html '''Click''' aquí si no se ve bien la escena]</center> | + | |
| - | + | ||
| - | Prueba a cambiar el valor de <math>k\;</math> y compáralas con <math>f(x)\;</math>: | + | |
| - | + | ||
| - | *<math>k=2 \ \rightarrow \ f(x)+2=x^2+2 </math>. | + | |
| - | *<math>k=-3 \ \rightarrow \ f(x)-3=x^2-3</math> | + | |
| - | + | ||
| - | Prueba a cambiar también la función <math>f(x)=x^2\;</math> por otras funciones, por ejemplo, <math>f(x)=x^3\;</math>. | + | |
| - | + | ||
| - | No olvides pulsar "Intro" al cambiar cada función. | + | |
| - | }} | + | |
| - | }} | + | |
| - | {{p}} | + | |
| - | + | ||
| - | ==Simetría respecto del eje X== | + | |
| - | {{Caja_Amarilla|texto=Las gráficas de las funciones <math>f(x)\;</math> y su opuesta, <math>-f(x)\;</math>, son simétricas respecto del eje de abscisas.}} | + | |
| - | {{p}} | + | |
| - | {{AI2|titulo=Actividad Interactiva: ''Función simétrica respecto del eje X''|cuerpo= | + | |
| - | {{ai_cuerpo | + | |
| - | |enunciado='''Actividad 1.''' Representación gráfica de una función <math>f(x)\;</math> cualquiera y de su simétrica <math>-f(x)\;</math>. | + | |
| - | |actividad= | + | |
| - | En esta escena tienes la gráfica de la función <math>f(x) = x^2-2x\;</math> (en verde) y la de su simétrica <math>-f(x)=-(x^2-2x)\;</math> (en amarillo). | + | |
| - | + | ||
| - | {{p}} | + | |
| - | <center><iframe> | + | |
| - | url=http://maralboran.org/web_ma/descartes/Analisis/El_pinta_graficas/grafic_4b.html | + | |
| - | width=450 | + | |
| - | height=380 | + | |
| - | name=myframe | + | |
| - | </iframe></center> | + | |
| - | <center>[http://maralboran.org/web_ma/descartes/Analisis/El_pinta_graficas/grafic_4a.html '''Click''' aquí si no se ve bien la escena]</center> | + | |
| - | + | ||
| - | Prueba a cambiar la función <math>f(x)=x^2-2x\;</math> por otras funciones, por ejemplo, <math>f(x)=\sqrt{x}\;</math>. (Para la raíz cuadrada debes escribir '''sqrt(x)'''). | + | |
| - | + | ||
| - | No olvides pulsar "Intro" al cambiar cada función. | + | |
| - | }} | + | |
| - | }} | + | |
| {{p}} | {{p}} | ||
| + | *'''Simetría respecto del eje Y:''' Las gráficas de las funciones <math>f(x)\;</math> y <math>f(-x)\;</math> son simétricas respecto del eje de ordenadas.}} | ||
| ==Dilatación y contracción== | ==Dilatación y contracción== | ||
| {{Caja_Amarilla|texto= | {{Caja_Amarilla|texto= | ||
| Línea 61: | Línea 16: | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| - | {{AI2|titulo=Actividad Interactiva: ''Dilatación y contracción de una función''|cuerpo= | ||
| - | {{ai_cuerpo | ||
| - | |enunciado='''Actividad 1.''' Representación gráfica de una función <math>f(x)\;</math> cualquiera y de su transformada <math>k \cdot f(x)\;</math>. | ||
| - | |actividad= | ||
| - | En esta escena tienes la gráfica de la función <math>f(x) = \sqrt{x}\;</math> (en verde) y la de su dilatada <math>2 \cdot f(x)=2 \cdot \sqrt{x} \;</math> (en amarillo). | ||
| - | |||
| - | {{p}} | ||
| - | <center><iframe> | ||
| - | url=http://maralboran.org/web_ma/descartes/Analisis/El_pinta_graficas/grafic_4e.html | ||
| - | width=450 | ||
| - | height=380 | ||
| - | name=myframe | ||
| - | </iframe></center> | ||
| - | <center>[http://maralboran.org/web_ma/descartes/Analisis/El_pinta_graficas/grafic_4e.html '''Click''' aquí si no se ve bien la escena]</center> | ||
| - | |||
| - | Prueba a cambiar el valor de <math>k\;</math>: | ||
| - | *<math>k=\cfrac{1}{2} \ \rightarrow \ \cfrac{1}{2} \cdot f(x)=\cfrac{1}{2} \cdot \sqrt{x} \ </math>. Obtendrás una contracción de <math>f(x)\;</math>. | ||
| - | *<math>k=-\cfrac{1}{2} \ \rightarrow \ -\cfrac{1}{2} \cdot f(x)=-\cfrac{1}{2} \cdot \sqrt{x} \ </math>. Obtendrás una contracción de <math>f(x)\;</math>, combinada con simetría respecto del eje X. | ||
| - | *<math>k=-2 \ \rightarrow \ -2 \cdot f(x)=-2 \cdot \sqrt{x} \ </math>. Obtendrás una dilatación de <math>f(x)\;</math>, combinada con simetría respecto del eje X. | ||
| - | |||
| - | |||
| - | Prueba a cambiar la función <math>f(x)=\sqrt{x}\;</math> por otras funciones, por ejemplo, <math>f(x)=sen(x)\;</math>. | ||
| - | |||
| - | No olvides pulsar "Intro" al cambiar cada función. | ||
| - | }} | ||
| - | }} | ||
| - | {{p}} | ||
| - | |||
| - | ==Traslación horizontal== | ||
| - | {{Caja_Amarilla|texto=Sea <math>f(x)\;</math> una función y <math>k>0\;</math> un número real, entonces la gráfica de la función <math>f(x+k)\;</math> se obtiene a partir de la de <math>f(x)\;</math> desplazándola <math>k\;</math> unidades hacia la izquierda y la de <math>f(x-k)\;</math> desplazándola <math>k\;</math> unidades hacia la derecha.}} | ||
| - | {{p}} | ||
| - | {{AI2|titulo=Actividad Interactiva: ''Traslación horizontal de una función''|cuerpo= | ||
| - | {{ai_cuerpo | ||
| - | |enunciado='''Actividad 1.''' Representación gráfica de una función <math>f(x)\;</math> cualquiera y de su transformada <math>f(x \pm k)</math>. | ||
| - | |actividad= | ||
| - | En esta escena tienes la gráfica de la función <math>f(x) = x^2+x-5\;</math> (en verde) y la de <math>f(x+1)=(x+1)^2+(x+1)-5\;</math> (en amarillo). | ||
| - | |||
| - | {{p}} | ||
| - | <center><iframe> | ||
| - | url=http://maralboran.org/web_ma/descartes/Analisis/El_pinta_graficas/grafic_4c.html | ||
| - | width=450 | ||
| - | height=380 | ||
| - | name=myframe | ||
| - | </iframe></center> | ||
| - | <center>[http://maralboran.org/web_ma/descartes/Analisis/El_pinta_graficas/grafic_4c.html '''Click''' aquí si no se ve bien la escena]</center> | ||
| - | |||
| - | Prueba a cambiar el valor de <math>k\;</math> y compáralas con <math>f(x)\;</math>: | ||
| - | |||
| - | *<math>Sumar \ k=2 \ \rightarrow \ f(x+2)=(x+2)^2+(x+2)-5 \ , \ f(x)-3=(x-3)^2+(x-3)-5</math>. | ||
| - | *<math>Restar \ k=3 \ \rightarrow \ f(x-3)=(x-3)^2+(x-3)-5</math>. | ||
| - | |||
| - | Prueba a cambiar también la función <math>f(x)=x^2+x-5\;</math> por otras funciones, por ejemplo, <math>f(x)=|x|\;</math>. (La función valor absoluto debes escribirla '''abs(x)'''). | ||
| - | |||
| - | No olvides pulsar "Intro" al cambiar cada función. | ||
| - | }} | ||
| - | }} | ||
| - | {{p}} | ||
| - | |||
| - | ==Simetría respecto del eje Y== | ||
| - | {{Caja_Amarilla|texto=Las gráficas de las funciones <math>f(x)\;</math> y su opuesta, <math>f(-x)\;</math>, son simétricas respecto del eje de ordenadas.}} | ||
| - | {{p}} | ||
| - | {{AI2|titulo=Actividad Interactiva: ''Función simétrica respecto del eje Y''|cuerpo= | ||
| - | {{ai_cuerpo | ||
| - | |enunciado='''Actividad 1.''' Representación gráfica de una función <math>f(x)\;</math> cualquiera y de su simétrica <math>f(-x)\;</math>. | ||
| - | |actividad= | ||
| - | En esta escena tienes la gráfica de la función <math>f(x) = x^2-2x\;</math> (en verde) y la de su simétrica <math>f(-x)=(-x)^2-2(-x)\;</math> (en amarillo). | ||
| - | |||
| - | {{p}} | ||
| - | <center><iframe> | ||
| - | url=http://maralboran.org/web_ma/descartes/Analisis/El_pinta_graficas/grafic_4d.html | ||
| - | width=450 | ||
| - | height=380 | ||
| - | name=myframe | ||
| - | </iframe></center> | ||
| - | <center>[http://maralboran.org/web_ma/descartes/Analisis/El_pinta_graficas/grafic_4d.html '''Click''' aquí si no se ve bien la escena]</center> | ||
| - | |||
| - | Prueba a cambiar la función <math>f(x)=x^2-2x\;</math> por otras funciones, por ejemplo, <math>f(x)=\cfrac{1}{x}\;</math>. | ||
| - | |||
| - | No olvides pulsar "Intro" al cambiar cada función. | ||
| - | }} | ||
| - | }} | ||
| ==Actividades== | ==Actividades== | ||
| {{Geogebra_enlace | {{Geogebra_enlace | ||
Revisión de 19:34 12 dic 2016
Tabla de contenidos |
Traslación vertical y horizontal
- Traslación vertical: Sea
 una función y
una función y 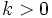 un número real, entonces la gráfica de la función
un número real, entonces la gráfica de la función 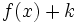 se obtiene a partir de la de
se obtiene a partir de la de  desplazándola
desplazándola  unidades hacia arriba y la de
unidades hacia arriba y la de 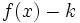 desplazándola
desplazándola  unidades hacia abajo.
unidades hacia abajo.
- Traslación horizontal: Sea
 una función y
una función y 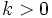 un número real, entonces la gráfica de la función
un número real, entonces la gráfica de la función 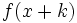 se obtiene a partir de la de
se obtiene a partir de la de  desplazándola
desplazándola  unidades hacia la izquierda y la de
unidades hacia la izquierda y la de 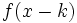 desplazándola
desplazándola  unidades hacia la derecha.
unidades hacia la derecha.
Simetría respecto de los ejes
- Simetría respecto del eje X: Las gráficas de las funciones
 y
y 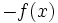 son simétricas respecto del eje de abscisas.
son simétricas respecto del eje de abscisas.
- Simetría respecto del eje Y: Las gráficas de las funciones
 y
y 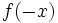 son simétricas respecto del eje de ordenadas.
son simétricas respecto del eje de ordenadas.
Dilatación y contracción
- Si
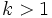 , la gráfica de la función
, la gráfica de la función 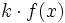 es una dilatación o estiramiento vertical de la gráfica de
es una dilatación o estiramiento vertical de la gráfica de  .
.
- Si
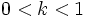 , la gráfica de la función
, la gráfica de la función 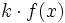 es una contracción o achatamiento vertical de la gráfica de
es una contracción o achatamiento vertical de la gráfica de  .
.
- Si
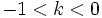 , la gráfica de la función
, la gráfica de la función 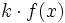 es la combinacion de una contracción y una simetría respecto del eje X.
es la combinacion de una contracción y una simetría respecto del eje X.
- Si
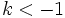 , la gráfica de la función
, la gráfica de la función 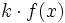 es la combinacion de una dilatación y una simetría respecto del eje X.
es la combinacion de una dilatación y una simetría respecto del eje X.
Actividades
En esta escena podrás practicar las transformaciones de funciones. Se te propondrán algunos ejercicios.

