Funciones arco (1ºBach)
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 19:00 13 dic 2016 Coordinador (Discusión | contribuciones) (→Función arcocoseno) ← Ir a diferencia anterior |
Revisión de 19:02 13 dic 2016 Coordinador (Discusión | contribuciones) (→Función arcocoseno) Ir a siguiente diferencia → |
||
| Línea 42: | Línea 42: | ||
| ==Función arcocoseno== | ==Función arcocoseno== | ||
| - | {{Tabla75|celda2=[[Imagen:arccos.jpg|thumb|250px|Funciones coseno y arcocoseno. Observa la simetría entre ambas.]] | + | {{Tabla75|celda2=[[Imagen:arccos.jpg|thumb|320px|Funciones coseno y arcocoseno. Observa la simetría entre ambas.]] |
| |celda1= | |celda1= | ||
| La función coseno no es inyectiva, pero si restringimos su dominio al intervalo <math>[0,\pi]\;</math> entonces es biyectiva y tiene inversa. A su inversa la llamaremos '''arcocoseno'''. | La función coseno no es inyectiva, pero si restringimos su dominio al intervalo <math>[0,\pi]\;</math> entonces es biyectiva y tiene inversa. A su inversa la llamaremos '''arcocoseno'''. | ||
| Línea 54: | Línea 54: | ||
| \\ | \\ | ||
| - | \, \qquad \qquad \qquad \ \ \ x \ \ \ \rightarrow \ \ \ \ y=arccos(x) | + | \, \qquad \qquad \qquad \ \ \ \ \ x \ \ \ \rightarrow \ \ \ \ y=arccos(x) |
| \end{matrix}</math></center> | \end{matrix}</math></center> | ||
| {{b}} | {{b}} | ||
| Línea 61: | Línea 61: | ||
| donde <math>arccos(x)\;</math> es el ángulo comprendido entre <math>0\;</math> y <math>\pi\;</math> tal que su coseno es igual a <math>x\;</math> | donde <math>arccos(x)\;</math> es el ángulo comprendido entre <math>0\;</math> y <math>\pi\;</math> tal que su coseno es igual a <math>x\;</math> | ||
| }} | }} | ||
| - | }} | ||
| - | |||
| {{p}} | {{p}} | ||
| {{Teorema_sin_demo|titulo=Propiedades|enunciado=La función arcocoseno tiene las siguientes propiedades: | {{Teorema_sin_demo|titulo=Propiedades|enunciado=La función arcocoseno tiene las siguientes propiedades: | ||
| Línea 69: | Línea 67: | ||
| *Es continua en su dominio. | *Es continua en su dominio. | ||
| *Su grafica es simétrica de la de su función inversa, el coseno, respecto de la bisectriz del primer cuadrante. | *Su grafica es simétrica de la de su función inversa, el coseno, respecto de la bisectriz del primer cuadrante. | ||
| + | }} | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
Revisión de 19:02 13 dic 2016
Menú:
| Enlaces internos | Para repasar o ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadoras |
Tabla de contenidos |
(Pág. 261)
Función arcoseno
La función seno no es inyectiva, pero si restringimos su dominio al intervalo ![[-\cfrac{\pi}{2},\cfrac{\pi}{2}\,]](/wikipedia/images/math/c/5/b/c5b617e52171199a746c52e69ba9da9b.png) entonces es biyectiva y tiene inversa. A su inversa la llamaremos arcoseno. entonces es biyectiva y tiene inversa. A su inversa la llamaremos arcoseno.
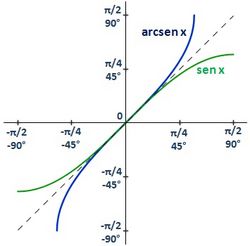
La función arcoseno se define como ![\begin{matrix} f:[-1,1] \rightarrow [-\cfrac{\pi}{2},\cfrac{\pi}{2}\,] \\ \, \qquad \qquad \qquad \ \ \ x \ \ \ \rightarrow \ \ \ \ y=arcsen(x) \end{matrix}](/wikipedia/images/math/c/2/1/c21cb86da8f59e167fb77175a689f552.png)
donde |
Propiedades
La función arcoseno tiene las siguientes propiedades:
![D_f=[-1,1]\;](/wikipedia/images/math/d/9/c/d9ce3f0aa136a3bc4dfce5325a11c16e.png) e
e ![Im_f=[-\cfrac{\pi}{2},\cfrac{\pi}{2}\,]](/wikipedia/images/math/5/5/4/55489a548259141a1e734bf3756c6971.png)
- Es continua en su dominio.
- Su grafica es simétrica de la de su función inversa, el seno, respecto de la bisectriz del primer cuadrante.
Función arcocoseno
La función coseno no es inyectiva, pero si restringimos su dominio al intervalo ![[0,\pi]\;](/wikipedia/images/math/0/3/3/0330944600b208d6f5f20d8e772dd7ce.png) entonces es biyectiva y tiene inversa. A su inversa la llamaremos arcocoseno. entonces es biyectiva y tiene inversa. A su inversa la llamaremos arcocoseno.
La función arcocoseno se define como ![\begin{matrix} f:[-1,1] \rightarrow [0,\pi]\, \\ \, \qquad \qquad \qquad \ \ \ \ \ x \ \ \ \rightarrow \ \ \ \ y=arccos(x) \end{matrix}](/wikipedia/images/math/6/6/f/66f0ea8fa1e7526b22d5cf748fe4f856.png)
donde | Imagen:Arccos.jpg Funciones coseno y arcocoseno. Observa la simetría entre ambas. |
Función arcotangente
La función tangente no es inyectiva, pero si restringimos su dominio al intervalo 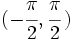 entonces es biyectiva y tiene inversa. A su inversa la llamaremos arcoseno. entonces es biyectiva y tiene inversa. A su inversa la llamaremos arcoseno.
La función arcotangente se define como 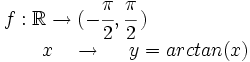
donde |
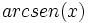 es el ángulo comprendido entre
es el ángulo comprendido entre 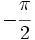 y
y 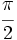 tal que su seno es igual a
tal que su seno es igual a 
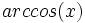 es el ángulo comprendido entre
es el ángulo comprendido entre 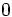 y
y 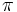 tal que su coseno es igual a
tal que su coseno es igual a ![Im_f=[0,\pi]\,](/wikipedia/images/math/d/d/7/dd763ac95a153560bac98798e8ccb15c.png)
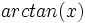 es el ángulo comprendido entre
es el ángulo comprendido entre