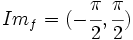Funciones arco (1ºBach)
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 19:05 13 dic 2016 Coordinador (Discusión | contribuciones) (→Función arcotangente) ← Ir a diferencia anterior |
Revisión de 19:07 13 dic 2016 Coordinador (Discusión | contribuciones) (→Función arcotangente) Ir a siguiente diferencia → |
||
| Línea 90: | Línea 90: | ||
| donde <math>arctan(x)\;</math> es el ángulo comprendido entre <math>-\cfrac{\pi}{2}</math> y <math>\cfrac{\pi}{2}</math> tal que su tangente es igual a <math>x\;</math> | donde <math>arctan(x)\;</math> es el ángulo comprendido entre <math>-\cfrac{\pi}{2}</math> y <math>\cfrac{\pi}{2}</math> tal que su tangente es igual a <math>x\;</math> | ||
| }} | }} | ||
| - | }} | ||
| - | |||
| {{p}} | {{p}} | ||
| {{Teorema_sin_demo|titulo=Propiedades|enunciado=La función arcotangente tiene las siguientes propiedades: | {{Teorema_sin_demo|titulo=Propiedades|enunciado=La función arcotangente tiene las siguientes propiedades: | ||
| - | *<math>D_f=\matbb{R}</math> e <math>Im_f=(-\cfrac{\pi}{2},\cfrac{\pi}{2})\,</math> | + | *<math>D_f=\mathbb{R}</math> e <math>Im_f=(-\cfrac{\pi}{2},\cfrac{\pi}{2})\,</math> |
| *Es continua en su dominio. | *Es continua en su dominio. | ||
| *Su grafica es simétrica de la de su función inversa, la tangente, respecto de la bisectriz del primer cuadrante. | *Su grafica es simétrica de la de su función inversa, la tangente, respecto de la bisectriz del primer cuadrante. | ||
Revisión de 19:07 13 dic 2016
Menú:
| Enlaces internos | Para repasar o ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadoras |
Tabla de contenidos |
(Pág. 261)
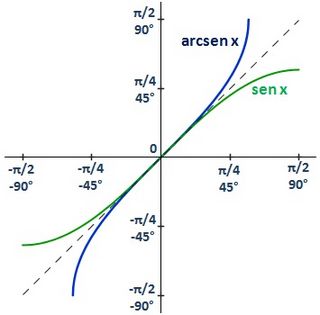
Función arcoseno
La función seno no es inyectiva, pero si restringimos su dominio al intervalo ![[-\cfrac{\pi}{2},\cfrac{\pi}{2}\,]](/wikipedia/images/math/c/5/b/c5b617e52171199a746c52e69ba9da9b.png) entonces es biyectiva y tiene inversa. A su inversa la llamaremos arcoseno. entonces es biyectiva y tiene inversa. A su inversa la llamaremos arcoseno.
La función arcoseno se define como ![\begin{matrix} f:[-1,1] \rightarrow [-\cfrac{\pi}{2},\cfrac{\pi}{2}\,] \\ \, \qquad \qquad \qquad \ \ \ x \ \ \ \rightarrow \ \ \ \ y=arcsen(x) \end{matrix}](/wikipedia/images/math/c/2/1/c21cb86da8f59e167fb77175a689f552.png)
donde |
Función arcocoseno
La función coseno no es inyectiva, pero si restringimos su dominio al intervalo ![[0,\pi]\;](/wikipedia/images/math/0/3/3/0330944600b208d6f5f20d8e772dd7ce.png) entonces es biyectiva y tiene inversa. A su inversa la llamaremos arcocoseno. entonces es biyectiva y tiene inversa. A su inversa la llamaremos arcocoseno.
La función arcocoseno se define como ![\begin{matrix} f:[-1,1] \rightarrow [0,\pi]\, \\ \, \qquad \qquad \qquad \ \ \ \ \ x \ \ \ \rightarrow \ \ \ \ y=arccos(x) \end{matrix}](/wikipedia/images/math/6/6/f/66f0ea8fa1e7526b22d5cf748fe4f856.png)
donde | Imagen:Arccos.jpg Funciones coseno y arcocoseno. Observa la simetría entre ambas. |
Función arcotangente
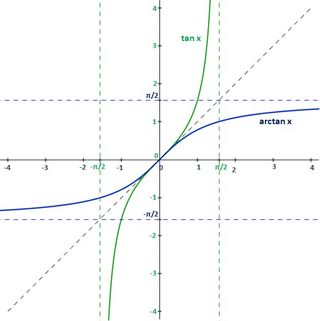
La función tangente no es inyectiva, pero si restringimos su dominio al intervalo 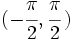 entonces es biyectiva y tiene inversa. A su inversa la llamaremos arcoseno. entonces es biyectiva y tiene inversa. A su inversa la llamaremos arcoseno.
La función arcotangente se define como 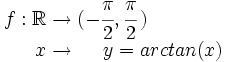
donde |
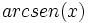 es el ángulo comprendido entre
es el ángulo comprendido entre 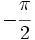 y
y 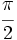 tal que su seno es igual a
tal que su seno es igual a 
![D_f=[-1,1]\;](/wikipedia/images/math/d/9/c/d9ce3f0aa136a3bc4dfce5325a11c16e.png) e
e ![Im_f=[-\cfrac{\pi}{2},\cfrac{\pi}{2}\,]](/wikipedia/images/math/5/5/4/55489a548259141a1e734bf3756c6971.png)
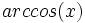 es el ángulo comprendido entre
es el ángulo comprendido entre 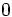 y
y 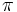 tal que su coseno es igual a
tal que su coseno es igual a ![Im_f=[0,\pi]\,](/wikipedia/images/math/d/d/7/dd763ac95a153560bac98798e8ccb15c.png)
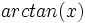 es el ángulo comprendido entre
es el ángulo comprendido entre 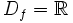 e
e