Plantilla:Cálculo de límites en el infinito (1ºBach)
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 21:52 17 dic 2016 Coordinador (Discusión | contribuciones) (→Comportamiento de una función cuando x tiende a infinito) ← Ir a diferencia anterior |
Revisión de 21:53 17 dic 2016 Coordinador (Discusión | contribuciones) (→Comportamiento de una función cuando x tiende a infinito) Ir a siguiente diferencia → |
||
| Línea 3: | Línea 3: | ||
| {{p}} | {{p}} | ||
| {{Caja_Amarilla|texto= | {{Caja_Amarilla|texto= | ||
| - | *<math>\lim_{x \to +\infty} f(x)=+\infty</math></center> si cuando x tienede a <math> + \infty</math>, los valores de <math>f(x)\;</math> se hacen tan grandes que no se pueden acotar. | + | *<math>\lim_{x \to +\infty} f(x)=+\infty</math> si cuando <math>x \to + \infty</math>, los valores de <math>f(x)\;</math> se hacen tan grandes que no se pueden acotar. |
| - | *<math>\lim_{x \to +\infty} f(x)=-\infty</math></center> si cuando x tienede a <math> + \infty</math>, los valores de <math>f(x)\;</math> se hacen tan pequeños y negativos que no se pueden acotar. | + | *<math>\lim_{x \to +\infty} f(x)=-\infty</math> si cuando <math>x \to + \infty</math>, los valores de <math>f(x)\;</math> se hacen tan pequeños y negativos que no se pueden acotar. |
| - | *<math>\lim_{x \to +\infty} f(x)=L \in \mathbb{R}</math></center> si cuando x tienede a <math> + \infty</math>, los valores de <math>f(x)\;</math> se hacen tan proximos a <math>L\;</math> como se quiera. | + | *<math>\lim_{x \to +\infty} f(x)=L \in \mathbb{R}</math> si cuando <math>x \to + \infty</math>, los valores de <math>f(x)\;</math> se hacen tan proximos a <math>L\;</math> como se quiera. |
| {{p}} | {{p}} | ||
| ---- | ---- | ||
Revisión de 21:53 17 dic 2016
Tabla de contenidos |
Comportamiento de una función cuando x tiende a infinito
Los posibles comportamientos de una función cuando x tiende a  (o a
(o a  ) son los siguientes:
) son los siguientes:
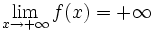 si cuando
si cuando  , los valores de
, los valores de  se hacen tan grandes que no se pueden acotar.
se hacen tan grandes que no se pueden acotar.
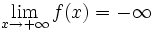 si cuando
si cuando  , los valores de
, los valores de  se hacen tan pequeños y negativos que no se pueden acotar.
se hacen tan pequeños y negativos que no se pueden acotar.
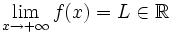 si cuando
si cuando  , los valores de
, los valores de  se hacen tan proximos a
se hacen tan proximos a 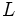 como se quiera.
como se quiera.
En ess tres definiciones se puede cambiar  por
por 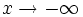 para obtener otras tres definiciones análogas.
para obtener otras tres definiciones análogas.
Límite de funciones polinómicas cuando x tiende a infinito
Límite de funciones inversas de polinómicas cuando x tiende a infinito
Límite de funciones racionales cuando x tiende a infinito
Video tutorial de matematicasbachiller.com
Video tutorial de matematicasbachiller.com
Video tutorial de matematicasbachiller.com
Ejemplos: Límite de una función racional en el infinito
Video tutorial de matematicasbachiller.com
Video tutorial de matematicasbachiller.com
Video tutorial de matematicasbachiller.com
Video tutorial de matematicasbachiller.com
Video tutorial de matematicasbachiller.com
Video tutorial de matematicasbachiller.com
Video tutorial de matematicasbachiller.com
Video tutorial de matematicasbachiller.com

